이제 본격적으로 스미스차트를 이용한 임피던스 매칭에 대해 공부해보겠습니다. 이것은 크게 RLC lumped 소자를 이용한 매칭과, Microstrip과 같은 전송선로를 이용한 매칭으로 나누어집니다. 우선 RLC를 이용한 매칭법을 마스터해보도록 하지요!
![]() 임피던스
매칭단 = Impedance Transformer
임피던스
매칭단 = Impedance Transformer
매칭을 시작하기 전에, 임피던스 매칭을 왜하는지 에 대해선 이미 보셨으리라 생각됩니다. 두 단간의 임피던스차이를 완충시켜서 최대한의 신호전력을 전달하기 위함입니다. 일반적으로는 그렇습니다.

그런데 많은 초심자 분들이 최대전력전달과 최대전력출력의 의미를 혼동하고 계십니다. 최대전력전달이란, 최대의 Gain을 내는 것을 의미합니다. 말그대로 입력에 들어간 것이 출력으로 최대한 뽑아낼 수 있어야 한다는, '전달'의 의미입니다. 반면 Power Amp에서 말하는 최대출력은 입력이 얼마가 들어왔건간에 출력단에서 흘릴 수 있는 최대 전류/전력을 의미하는 '용량'의 개념입니다. 혼동이 없으시길!
그러므로 최대전력전달이라는 개념은 손실없이 신호를 흐르게 하겠다는 의미로 Amp이외의 경우에 주로 사용되는 개념이고, Amp에서의 임피던스 매칭단은 아래의 그림에서 처럼 임피던스 변환기(impedance transformer)의 의미가 강합니다.

Amplifier 회로개념잡기에서 보셨듯이 무조건 최대전력전달을 꾀하기 보다는 목적에 맞게 잡음, 최대출력전달 등에 최적화된 임피던스가 따로 있기 때문입니다. 최대전력전달점이 아니라 각각의 목적에 맞게 해당 임피던스 점으로 임피던스를 매칭시켜 주어야 하지요.
그렇다면 우리가 임피던스 매칭을 한다는 것은 무엇을 의미할까요? 그것은 바로 서로 다른 임피던스단 간에 들어갈 소자값을 결정하고 찾는 과정을 의미하는 것이지요!
![]() 스미스
차트 궤적 이동
스미스
차트 궤적 이동
스미스차트를 이용한 임피던스 매칭에서 매칭 소자값은, 부하 임피던스가 정합점을 목표로 이동할 때의 궤적(trace)에 따라 결정되는 것입니다. 각각의 직병렬 소자에 따라 어떤 궤적을 움직이는지를 차근차근 알아보도록 하지요. 우선 스미스차트 상단이 양의 허수부분 Inductance, 하단이 음의 허수부분 Capacitance을 의미하기 때문에 아래와 같은 단순한 법칙이 성립됩니다.
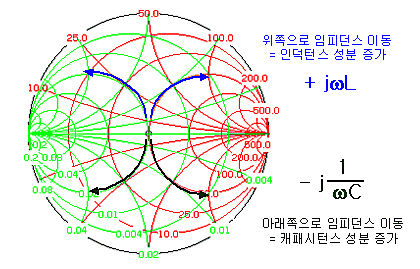
여기서 위/아래 방향의 의미는 보시다시피 실제로는 하나의 원상에서 시계방향이냐 반시계방향이냐를 의미합니다. 왜냐하면 원을 타고 위로 올라가는 것처럼 보이다가도 한참 원을 돌다보면 도로 내려오기도 하니까요. 이것은 스미스차트 자체가 극좌표구조라 그런 것이므로, 위(인덕턴스), 아래(캐패시턴스)라는 개념을 명확히 하기 위해 초심자들이 헷갈려하는 시계/반시계방향이란 용어보다 위 아래라는 용어를 사용하고 있습니다. 다만 어디까지나 같은 원주 상을 움직임을 명심하시기 바랍니다.
부하임피던스를 이동시킬 때 그 궤적이 원을 따라 위로 올라가면 매칭단에 인덕터 L소자를 추가하라는 의미고, 궤적이 원을 따라 아래로 내려가면 C소자를 추가하라는 의미가 됩니다. 이것에 대한 이해는 그리 어렵지 않은데, 이런 의문이 들 수 있습니다.
하필 왜 부하 임피던스 궤적은 특정 원을 따라 움직일까?
스미스차트 좌표계를 이해하면 쉽게 답이 나옵니다. 스미스차트상의 각각의 원들은 그 자체가 실수임피던스, 즉 저항 R의 좌표계를 의미합니다. 하나의 같은 원주상에서는 R값이 동일하다는 의미이지요. 스미스차트는 어디까지나 좌표계일 뿐입니다. 그러므로 L이나 C소자만 추가하는 LC 매칭에서는, 하나의 인덕터나 캐패시터를 추가할 때 L이나 C값만 변화할 뿐, R값은 변화하지 않으므로 항상 시작점과 같은 동일한 상수저항원을 따라 돌게 됩니다.
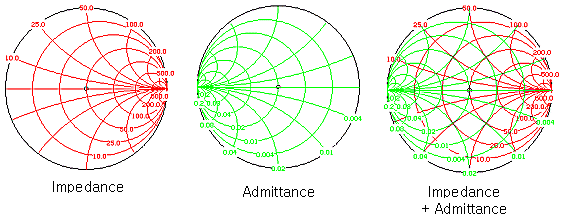
자, 여기까지는 직렬(Series) 연결에 대한 것입니다. 스미스차트 중 임피던스 차트만 이용했기 때문이죠. 병렬(shunt)소자를 추가할 때는 아래와 같이 임피던스 차트가 아닌, Y축 대칭된 어드미턴스 차트가 사용됩니다. 대부분의 스미스차트에는 임피던스차트와 어드미턴스 차트가 다른 색상으로 함께 인쇄되어 있지요. 어드미턴스 차트에서의 소자추가 역시 임피던스 차트일 때와 똑같습니다. 다만 어드미턴스차트의 실수 저항원들은 오른쪽이 아닌 왼쪽을 시작점으로 한다는 것이 다를 뿐입니다. 그리고 어드미턴스 역시 LC가 추가되면서 실수원상에서 허수부만 변화됩니다.
스미스차트 상의 4가지 기본적인 궤적을 종합하면 아래와 같이 정리됩니다.
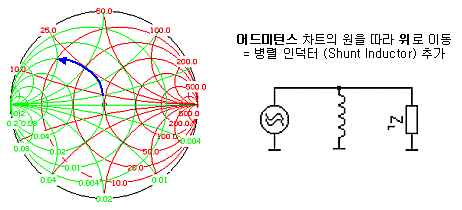
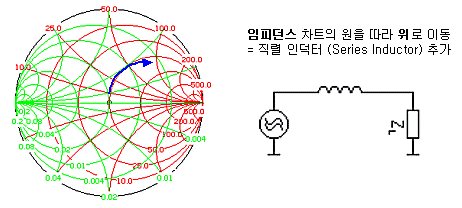
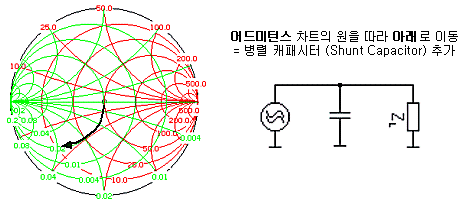
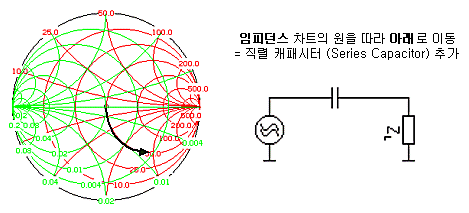
위의 4가지 궤적을 통해 우리는 어떠한 점에 존재한 부하임피던스라도 중심의 특성임피던스점으로 갖다놓을 수 있습니다. 상황에 따라 어떤 궤적을 선택하느냐는, 여러분들의 자유인 것이죠.
![]() 궤적
이동에 따른 소자값들
궤적
이동에 따른 소자값들
위에서 처럼 어떤 소자를 추가할지 결정되었다면, 과연 어떤 값을 가지는 소자를 달아야 할지 결정되어야겠지요? 그러기 위해서는 궤적이 움직인 상대적인 좌표값을 읽어야 합니다. 각각의 L, C 소자가 움직인 궤적의 이동거리를 읽은 후 그것을 아래와 같은 임피던스 수식을 통해 역으로 환산해야 하지요. 아래는 궤적에 따른 직렬 L값을 계산하는 방법의 사례입니다.
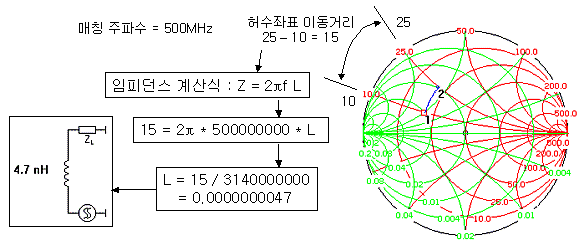
보다시피 계산법은 상당히 간단합니다. 그리고 상당히 귀찮습니다. -_-;
스미스차트종이와 컴파스를 이용한 완전한 Hand 매칭때는 계산기를 들고 저런 귀찮은 계산을 열심히 해야하지만, 우리는 이제 Smith tool이란 것을 알았기 때문에 더 이상 단순한 계산을 할 필요는 없습니다. Smith tool을 이용하면 Schematic 창에 그 결과 회로모양과 소자값을 바로 계산해서 일러주니까요. 어째서 이런 소자값들이 계산되는지 정도만 알아도 충분합니다.
![]() 저항(R)을
통한 스미스 차트 궤적 이동
저항(R)을
통한 스미스 차트 궤적 이동
우리는 이제껏 LC 직병렬 소자 추가에 따른 임피던스 매칭에 대해 알아보았습니다. 그런데 R소자 추가에 따른 매칭에 대해서는 위에서 같이 언급하지 않는게 뭔가 수상하지 않습니까? 수상함을 못느끼셧다면 지금부터 얼른 수상하시기 바랍니다.(-_-a?)
물론 R을 이용한 매칭에 대해 따로 다루는 이유가 있습니다. 저항소자 R을 추가할 때 부하 임피던스는 아래와 같이 움직이게 됩니다.
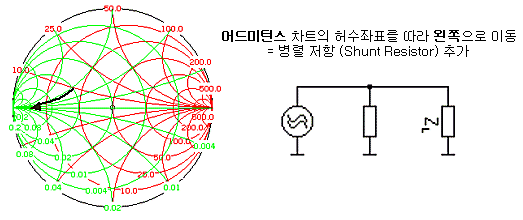
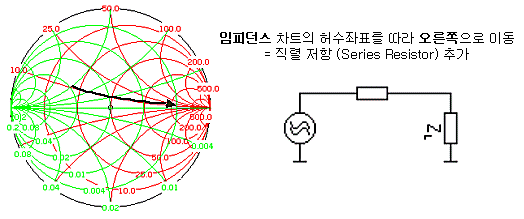
LC 소자 추가할 때와는 정반대로, 동일한 허수임피던스/어드미턴스 좌표상을 움직이게 되지요. 허수부는 고정되고 실수 임피던스만 변화하게 되기 때문입니다. 매칭할 때 저항을 직접 달아서 매칭에 이용하면 편리한 경우가 많이 있습니다. 임피던스 점을 움직일 수 있는 궤적형상이 추가되기 때문에 좀더 수월하게 임피던스 점을 옮길 수 있겠지요?
그렇지만 꼭 상기해야 할 것이 있습니다. 저항은 실제로 에너지를 소모하고, 잡음원이 된다는 사실입니다. 그렇기 때문에 일단 잡음에 민감하고 출력전력에 민감한 매칭단 - 예를 들어 LNA 입력단이나 Power amp 출력단 - 에서는 저항을 이용하여 매칭하는 것은 아주 위험한 행위가 됩니다.
LC 소자는 이론적으로 소위 reactance 소자이기 때문에 실제로 에너지를 소모하는 것이 아니라, 전기장과 자기장으로 에너지를 잠시 축적하는 무손실성 소자입니다. 물론 L, C 모두 실제로는 작은 저항성분을 갖고 있긴 합니다만, 진짜 R에 비하면 새발의 피입니다. 그래서 일반적인 임피던스 매칭은, LC 소자만으로 구현하는 것이 정상이고, 가장 경제적으로 손실이 없는 매칭이 구현됩니다.
대신에 R 소자가 잡음/전력특성을 갉아먹긴 한데, 사용한 부위에 따라 발진을 잡아주고 회로를 안정화시킬 수 있는 역할을 하기도 합니다. 결국 발진을 잡는다는 것은 저항으로 인해 전체적으로 약간씩 에너지를 깎아먹는 효과로 인해 미세한 발진원을 사전에 죽이는 듯한 기능을 하는 것입니다. 또한 경우에 따라서는 임피던스 점이 아주 애매한 곳에 위치해서 작은 저항이라도 써서 부하 임피던스 점을 이동시키고 매칭해야 하는 경우도 있습니다.
다시말해서, 매칭에서 R 소자를 직접 사용하는 것은 왠만하면 자제하고, 꼭 필요한 곳에만 사용해야 한다는 것입니다. 발진문제가 별로 없으면 굳이 억지로 발진제어용 R을 달 필요가 없고, R 없이도 매칭이 가능하다면 그냥 안쓰는게 속편합니다. 그렇다고 식탁위의 바퀴벌레 보듯이 R소자를 무조건 멀리해서도 안되겠죠. 필요한 경우에 정확히 사용하는 기지도 필요하므로 각자가 고민해보셔야 할 문제입니다.
![]() Conjugate
Matching
Conjugate
Matching
여기서의 모든 설명은, 부하임피던스 점을 중심에 갖다놓는 load -> source 방향의 매칭을 논하고 있습니다. 상황에 따라 source에서 load로 향하는 반대방향의 매칭도 가능하며, 중심점을 해당 목표점으로 움직일 수 있도록 궤적을 그리면 됩니다. 또한 어느 방향으로 매칭하느냐는 아무런 상관이 없습니다. 회로를 찾는 순서만 바뀔 뿐이니까요!
다만, 중심에만 갖다 놓는 매칭을 하다보면 깜박하게 되는 무언가가 있습니다. 바로 conjugate matching입니다. 원래 매칭할 때는 맞추고자 하는 상대편 임피던스의 켤레 복소수, 즉 허수부 부호를 바꾼 임피던스 점에 갖다 맞춰야 합니다. 왜일까요??
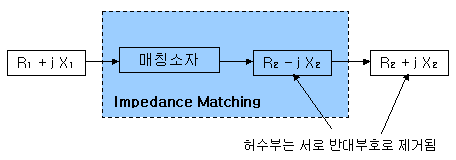
임피던스 매칭의 주요한 핵심은, 어떤 단일화된 특성 임피던스로 양단을 통일한다는 데 있습니다. 그러기 위해서는 허수부가 제거된 실수 임피던스로 남아야 하기 때문입니다. 예를 들어 50옴에서 20+j12쪽으로 매칭시키려면, 20+j12 가 아니라 20-j12 임피던스 점으로 가도록 궤적을 만들어야 합니다. 이렇게 하면 최종단에서는 변화된 20-j12 와 원래 있던 20+j12 가 같은 point에 놓이면서 허수부가 서로 더하고 빼져서 상쇄가 되고 실수부 20만 남게 됩니다. 그렇기 때문에 원래 매칭은 목적지의 켤레복소수 값에 맞추게 되는 것이지요.
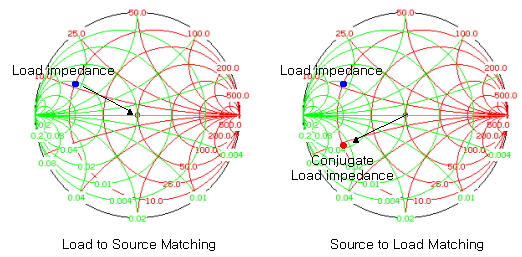
그런데 중심점, 즉 50옴 임피던스 점은 50+j0 으로 허수부가 없는 상태입니다. 그래서 허수부의 부호를 바꿀 필요도 없기 때문에 그냥 아무 생각없이 중심에만 갖다 놓아도 매칭이 되는 것이죠. 사실은 이것도 conjugate matching을 하고 있는 것입니다. 굳이 따지자면 50-j0 에다 매칭시키는 상황이라고 볼 수도 있지만, 어차피 있지도 않은 숫자의 부호를 바꾼다는 것은 별로 의미없는 일입니다.
고로 50옴이 아닌 점을 목적지로 스미스차트상에 거꾸로 궤적을 그리게 된다면, 반드시 목적지를 켤레복소수 임피던스 점으로 찍고 매칭해야 합니다. 결국 위의 그림처럼 스미스차트의 가로축에 대칭한 점을 찍고 매칭시켜주면 되는 문제입니다. 물론, 어떻게 하느냐는 여러분의 판단인데 일반적으로는 Load -> Source Matching이 더 편하기 때문에 많이 사용합니다.
![]() 어떤
궤적을 선택할 것인가?
어떤
궤적을 선택할 것인가?
자, 그런데 과연 어떤 궤적을 이용하여 매칭해야 할까요? 이 질문은 다시 말해 어떤 소자배치를 이용하여 매칭하느냐에 대한 문제를 언급하는 것입니다. 왜냐하면, 정해진 부하 임피던스를 정합점으로 이동하는 방법의 수는 한가지만이 아니기 때문입니다. Smith tool 예제에 사용했던 20+j12를 50옴에 정합하는데는 아래와 같이 여러 방법이 존재합니다.
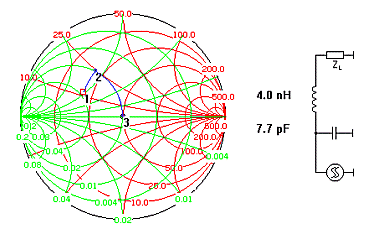
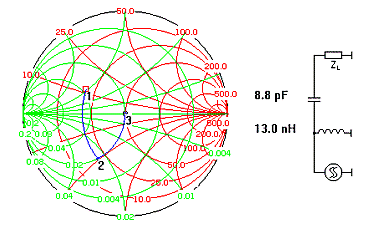
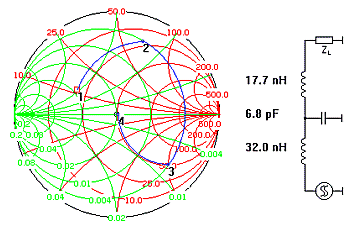
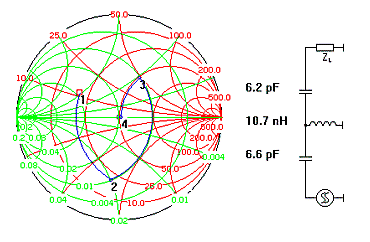
소자수와 배열을 늘려가면 끝도 없이
많은 방법이 나옵니다.
그렇다면 이런 궁금증이 생기지 않을
수 없습니다.
그렇다면 대체 어떤 형태의 매칭을 골라야 하는감?
이 질문에 대한 정답은 없습니다. 상황에 따라 어떤 특성을 가진 매칭구조를 쓸 것인지는 사용자가 선택해야 할 문제입니다. 대신에 어떤 기준을 적용할 수 있는지 기준을 한번 보도록 하지요.
▶ 단수는 가능하면 적게
소자
많이 붙여서 단가 높이면 좋아할 사장님이 있을까요? (^^;) 간결하게
매칭해야 나중에 요상한 변수를 줄일 수 있겠지요. 일반적으로 L하나,
C하나씩 두 개의 직병렬 소자로 2 단 매칭하는 경우가 가장 일반적이고
흔합니다.
만약 임피던스 점이 아주 낮거나 하도 이상한 곳에 가있다면, 어쩔 수 없이 3단을 써야 할 수도 있겠죠. 또한 3단 매칭 (Pi 혹은 Ti 형태)은 일정한 Q값을 유지해야할 때 용이해서 쓰기도 합니다. 그리고 저 아래에 언급되겠지만, 대역폭 문제로 4단 소자 이상으로 매칭할 수도 있긴 합니다. 특별한 조건이 없는한, 두 개만으로 매칭해야겠죠?
▶ LPF 형태, HPF 형태
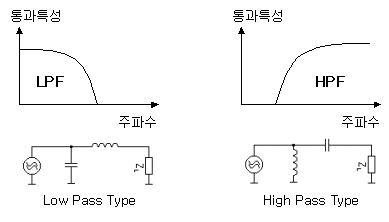
가장 일반적으로 많이 사용하는 형태는 위와같이 LPF 와 HPF의 형태입니다. 그중에서도 LPF 형태가 가장 널리 사용되는 편인데, RF신호를 처리하면서 발생하는 각종 하모닉 성분들을 필터링 할 수 있기 때문입니다. HPF구조의 경우는 저주파 발진신호를 좀더 잘 잡을 수 있다는 장점과 함께, LPF와 함께 사용되어 신호처리 주파수대역을 좀더 명확하게 조절할 수 있습니다.
우리가 임피던스 매칭을 할 때 한가지 알 수 있는 것은, 매칭을 시키는 특정 주파수가 존재한다는 것입니다. 모든 주파수에서 매칭시킨다는 것은 매우 어려운 일이고, 보통 어떤 중심주파수를 놓고 매칭을 하게 되는 것이죠. 그래서 임피던스 매칭은 어떤 면에서 본다면, 특정 주파수만 잘 통과시키는 효과적인 필터를 구현하는 것과 매우 유사하다는 대목을 잘 유념해둘 필요가 있습니다. 임피던스 매칭단은 위와 같이 필터틱한 통과특성을 가지고 불필요한 주파수대역의 에너지를 매칭주파수 대역으로 몰아주는 역할을 하는 것처럼 보이게 되는 것이지요.
▶ 소자값을 고려
궤적이 된다고
해서 무조건 그 소자값을 쓸 수 있는지 알 수 없으니, 소자값도 고려해가며
궤적을 고려해볼 필요는 있습니다. 저 밑에 따로 설명됩니다.
▶ 대역폭을 고려
대역폭을 늘이기 위해서는 궤적을 작게 움직이고, 대역폭을 좁혀야 한다면 궤적을 많이 움직일 수 있는 매칭을 하는 것이 유리합니다. 바로 아래 설명을 보시지요!
![]() 대역폭
대역폭
임피던스 매칭은 특정한 중심주파수에서 이루어지며, 그 주파수에서 멀어질수록 매칭이 깨집니다. 그렇다면 이러한 매칭 대역폭은 무엇과 관련되게 될까요? 그것은 회로의 Q값과 관련되게 됩니다.
그놈의 Q값이 참 여기저기서 나오는데, 알쏭달쏭하시나요? 다른 기초강의글들을 죽 봐오신 분들은 아시겠지만, Q는 크게 두가지 의미가 있습니다. L,C 소자 강의편에 설명된 것처럼 소자의 loss를 알려주는 Q와, 대역폭을 의미하는 Q가 있습니다. 스미스차트에서의 Q는 둘다 의미가 상통하게 표현될 수 있지만, 그중에서 대역폭이란 개념을 중점에 두고 따져보도록 하겠습니다. 우선 대역폭을 의미하는 Q는 아래와 같은 수식적 구조를 가집니다.
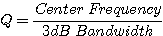
중심주파수와, 그 중심주파수 크기에서 양쪽으로 반씩 떨어진 주파수지점간의 간격(3dB bandwidth)의 비를 의미합니다. 그러므로 Q가 낮을수록 매칭이 이루어지는 대역폭이 넓다는 뜻입니다. 소자의 품질을 따지는 Q와 달리 이런 회로의 대역폭 Q는 높은게 좋은지 낮은게 좋은지에 대한 기준은 없습니다. 상황에 따라 광대역을 구현해야 하는지 협대역을 구현해야 하는지에 따라 다르게 되지요.
자, 그리고 스미스차트에서 표현되는 Q는 아래와 같습니다.
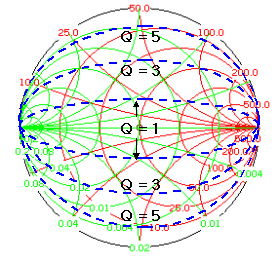
눈치가 빠른 분이라면, 이게 무얼 의미하는지
아시겠죠? 좀더 실제적으로 아래의 그림를 보시지요!
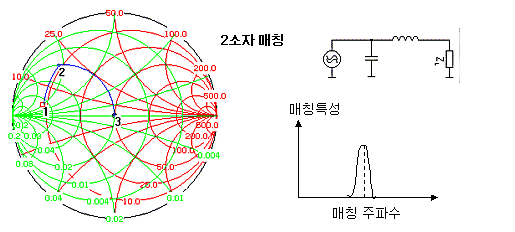
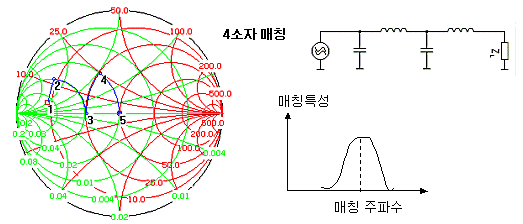
그렇습니다. 소자를 여러개 쓰면, 스미스차트가 움직이는 궤적을 수평축에 가깝게, 낮게 칠 수가 있게 됩니다. 즉 Q값이 낮아지면서 대역폭은 넓어지는 것입니다. 언뜻 보면 높이차이가 그리 크지 않은 것 같아보여도, 실제로 매칭이 가능한 주파수폭을 넓힐 수 있는 중요한 방법입니다.
아래의 S파라미터 그래프는 Q값을 낮게 가져가는 다단매칭의 실제 사례로써, 매칭소자를 많이 사용하여 궤적을 낮게 칠수록 대역폭이 늘어나고 있는 것을 보여주는 사례입니다. 1GHz를 중심주파수로 하고 VSWR이 1.5:1 정도 되는 경우를 정매칭으로 가정하고, VSWR이 1.5:1 일 때의 S11값인 -13.8dB를 기준으로 한 매칭 대역폭을 계산하였습니다.
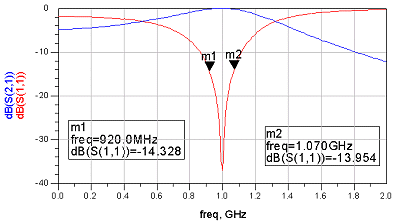
(a)
2 소자로 매칭한 경우 - Mathcing BW : 150 MHz
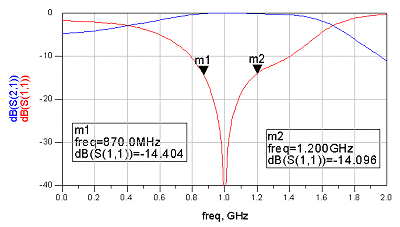
(b)
4 소자로 매칭한 경우 - Mathcing BW : 330 MHz
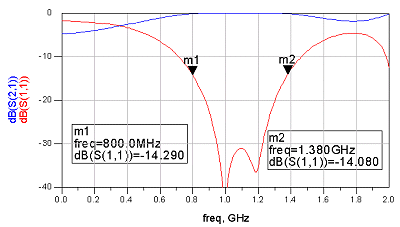
(c)
6 소자로 매칭한 경우 - Mathcing BW : 580 MHz
보시다시피 소자수를 늘려가며 Q를 낮춘 매칭의 경우 S11의 매칭폭이 점점 더 넓어짐을 알 수 있습니다. 즉, 더 넓은 주파수에서 반사를 최소화하면서 신호를 전송한다는 의미로써, 매칭이 광대역화 되었다는 의미가 됩니다.
![]() 소자값은
맘대로 안돼~ ㅠ.ㅠ
소자값은
맘대로 안돼~ ㅠ.ㅠ
지금까지 우리가 둘러본 매칭과정은, 사용자 맘대로 소자수와 궤적의 형태만 정하면 되는 것처럼 보입니다. 하지만, 현실은 그렇지 않습니다. 예를 들어 매칭을 해서 11.3 pF의 캐패시터가 필요하다고 치지요. 하지만 그런 애매모호한 소자값을 팔지 않습니다. 그렇다면 73nH의 인덕처럼 딱 떨어지는 인덕터를 구한다면? 그것 역시 시중에서 구하기 애매한 값입니다.
실제로 땜질을 해보신 분들은 아시겠지만, 캐패시터와 인덕터는 어느정도 정해진 값의 소자들을 써야 합니다. 일반적이고 뻔한 1.2, 1.5, 1.8, 2.2, 2.7, 3.3, 3.9, 4.7, 5.6, 6.8, 8.2, 10, 12, 15, 18, 22, 27, 33, 39, 47, 56, 68, 82, 100 ... 와 같은 식의 소자값들이 많습니다. 물론 그 이외에 있는 소자값들도 있지만, 수중에 사용가능 또는 계획된 소자들의 값들이 얼마인지 미리 알아놓을 필요가 있지요.
고로 LC 매칭시에는 반드시 위 소자값들과 딱딱 떨어지는 궤적을 그릴 수 있도록 만들어야 유리합니다. 중요한 문제이죠. 아무리 혼자서 손으로 혹은 툴을 이용해 매칭한다 한들 그 소자값이 없다면 말짱 도루묵이니까 다시 노가다를 해야 합니다.
또 이런 제한된 소자값들 때문에 완벽하게 중심에 갖다놓는 매칭이 쉽지가 않습니다. 원하는 궤적을 그리기 보다는 소자값에 맞춘 매칭을 해야 한다는 것이 LC lumped 매칭의 큰 약점중의 하나입니다. 물론 이것도 맨날 해보면 익숙해져서 소자값이 딱딱 떨어지게 잘 되긴 하지만요. ^^;
![]() LC
매칭, 알고보면 열나 쉽다
LC
매칭, 알고보면 열나 쉽다
스미스차트는 도구이고, 위와 같은 배경지식을 바탕으로 하면 LC 두 개로 어떤 상황에서도 매칭을 구현할 수 있습니다. 물론 매칭과 관련한 각종 테크닉들이 존재하지만, 위에 열거된 기본지식만으로도 매칭하는데는 아무런 불편함이 없습니다. 실제적인 매칭에 대한 사례는 Smith tool 사용법을 통해 감을 잡으시고, 위의 배경지식을 토대로 좀더 깊이이는 매칭을 구현해보시기 바랍니다.
Copyright by RF designhouse. All rights reserved.