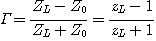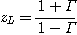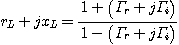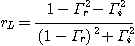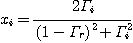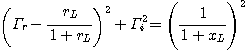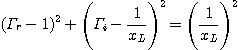스미스
차트란?
1939년
Philip F. Smith가 transmission line의 편리한 계산을 위해 만들어낸 것으로, 현재
전세계 수많은 RF 엔지니어들이 애용하는 그래픽 포맷이자 도구이다. 최근에는 RF
tool의 발달으로 스미스 차트를 이용한 손계산은 점차 적어지고는 있지만, 각종 결과를
스미스 차트에 출력해봄으로써 transmission line의 행동특성을 들여다 볼 수 있기
때문에 아직까지 업계 전반에서 사용되고 있다.
스미스 차트는 직교 좌표계를 한쪽점을 기준으로 원좌표로 변환한 것으로 보면된다. 반사계수와 부하 임피던스(load impedance)와의 관계식을 정리해보면 복소수의 원의 공식으로 변환이 가능하고, 이것을 단계별로 plotting시키면 된다. 그런데 이렇게 원좌표로 변환하고 나면, 직교좌표계에서 볼 수 없었던 몇가지 편리한 점이 나타나서 유용하게 활용할 수 있게 된다. 복소 직교좌표계에서는 사방이 무한 대로 뻗어나가기 때문에 어느정도 범위까지 한정된 그래프를 그려야 하지만, 원좌표로 하게되면 무한 대의 위치까지 nonlinear한 scale로 둥근 원 안에 다 표현할 수 있다. 바로 이러한 점이 스미스 차트와 같은 원좌표 형상의 중요한 장점중 하나이며, 각 실수 또는 허수의 수치변화가 스미스 차트 내에서 임의로 움직이는 것이 아니라 그려진 궤적형상과 동일하게 이동한다는 점을 통해 계산기 없이도 여러 복소변환 계산을 가능하게 한다.
스미스 차트의
사용법
RF를 시작한지 얼마 안되는 사람이라도 스미스차트를 본적 없는 사람은 별로 없으리라 생각된다. 스미스 차트 생성의 원리같은 것은 수식적으로도 간단하지만, 중요한 것은 그 원리나 이론이 아니라 스미스 차트를 어떤 용도로 어떻게 사용하느냐인 것 같다.
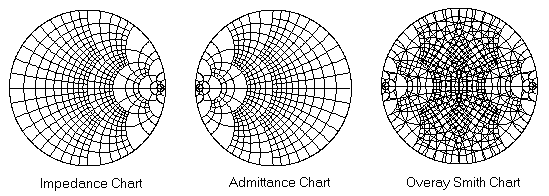
스미스 차트상에 올라가는 그래프나 점은 주로 복소 임피던스 값이나 S파라미터 값이 올라가게 된다. 일단 복소 임피던스를 plot하여 사용하면 곧바로 반사계수와 SWR을 읽을 수 있기 때문에 임피던스 매칭용으로 쉽게 사용이 가능하고, S 파라미터를 plot하면 주파수별 S 파라미터의 궤적을 통해 다양한 정보를 얻을 수 있다. 아래에 스미스 차트의 각 수치의 의미를 그림으로 나타내었다.
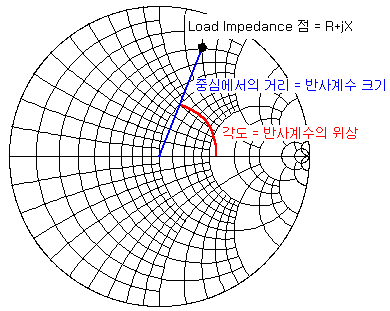
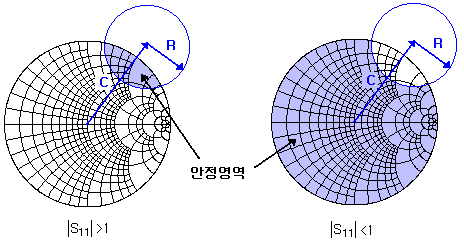
스미스 차트에서 오른쪽부터 시작되는 원의 직경은 실수부를 의미하고, 오른쪽 끝에서 사방으로 퍼져나가는 모양의 곡선은 허수부를 의미한다. 복소 부하 임피던스 ZL은 그림과 같이 스미스 차트 상에서 어느 한점으로 표시되는데, 중앙에서 이 점까지의 거리 R과 스미스차트 전체의 직경의 비율은 반사계수의 크기를 의미하며, 오른쪽 끝단에서 점까지의 각도가 반사계수의 위상을 의미한다. 결국 반사계수나 부하 임피던스 중 어느 한가지를 알면 나머지는 점을 찍는 순간 바로 알 수 있게 된다.
임피던스 정합의 경우에는 이러한 부하 임피던스를 원의 중앙, 즉 임피던스가 1인 지점까지 실수와 허수 궤적으로 따라 움직이도록 하는 것이 목표가 되며, 그 움직인 거리에 따라 LC값이나 stub의 길이가 곧바로 추출되므로 아주 편리하다. 이 경우 사용상의 편리를 위해 스미스차트를 반대로 뒤집어서 사용하기도 하는데, 일반적인 직렬연결용으로는 임피던스 차트를, 병렬연결의 경우는 어드미턴스차트를 이용하여 곧바로 설계하면 편리하다. 보통 스미스차트는 이 두 가지 종류의 차트를 색깔을 다르게 하여 한 종이에 print하여 사용하는 경우가 많은데, 그런 경우 이동중인 부하 임피던스 점 위에서 곧바로 직렬-병렬 변환이 가능하기 때문에 유리하다.
