스미스차트, 그 뒷이야기

스미스차트, 그 뒷이야기

지금까지 스미스차트와 임피던스 매칭과 관련하여 알아야할 여러 가지 기본들을 배웠습니다. 마지막으로 몇가지 실제적으로 고려해야 할 문제들과 스미스차트의 부가적인 기능들을 알아보면서 스미스차트 기초강의를 마치도록 하겠습니다.

LC매칭의 마무리

"음? 왠 마무리? 스미스차트로 임피던스점 돌려서 LC값 찾고 땜질하면 끝이 아니었나?"
이런 생각이 드실지도 모릅니다만, 마무리란 얘기가 따로 또 나온다는 것은 아직 끝난 게 아니란 의미입니다. 자, 이쯤에서 한가지 명심할 것이 있습니다.

스미스차트로 뽑은 매칭값의 결과는 현실에서 완전히 똑같지 않다

참으로 매정하지만, 그냥 스미스차트로 LC값을 찾아서는 절대로 똑같이 나오지 않습니다. 왜그럴까요? 단순히 소자값이 부정확해서일까요? 우리가 스미스차트를 돌려서 찾는 L,C값은 완전히 이상적인 소자값이라는 점이 문제입니다. 어떤 저항성 소모성분이나 기생 리액턴스 성분이 존재하지 않는 완벽한 인덕터와 캐패시터 값이라는 것이죠.

하지만 고주파에서의 LC 강의 섹션에서 보셧듯이, 실제 인덕터/캐패시터 소자들은 기생성분들로 인해 SRF가 존재하고, 또 자체적인 작은 저항성분으로 인해 손실이 존재합니다. 이런 부가적인 문제들로 인해 스미스차트에서 찍어주는 이상적인 L,C 값만으로는 매칭을 구현하면 그 결과가 어리부리하게 됩니다. 그럼 대체 어떻게 해야 할까요?

시뮬레이터가 없는 경우라면 어쩔 수 없이 실제로 소자들값을 비슷한 값들로 교체해가며 땜질해서 정확한 결과값을 다시 찾는 튜닝을 해야 합니다.

하지만 다행히도, 이제 고주파 회로 설계에서는 시뮬레이터를 이용하는게 많이 보편화되어 있어서 매칭값의 보정이 쉬워졌습니다. 상용화된 RF 회로설계 프로그램들은 이상적인 L,C 말고도 실제의 인덕터/캐패시터 소자의 측정치 (S파라미터)를 라이브러리로 갖고 있습니다.

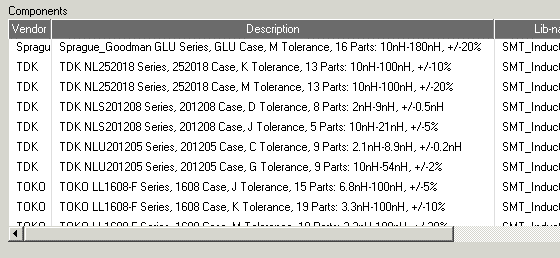
위의 ADS library 예제 그림처럼 각 소자값은 물론 제작사와 크기별로 다양한 라이브러리가 존재하며, 툴에 라이브러리가 없더라도 해당 소자 공급회사에서 라이브러리 파일을 만들어서 배포합니다.

그렇다면, 이상적인 LC값과 실제 소자값의 특성차이는 어떻게 나타나는지 예를 보도록 하겠습니다.

(a) 이상적인 L,C로 매칭값을 찾은 경우
(b) 같은 값의 실제 소자 라이브러리로 교체한 경우

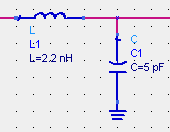
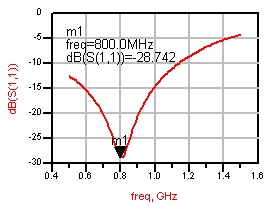
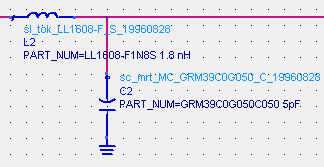
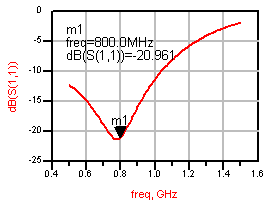
위에서 왼쪽은 그냥 LC 소자를 이용한 이상적인 매칭값의 결과이고, 오른쪽은 그것과 똑같은 소자값이되, 실제 사용할 소자의 주파수특성을 라이브러리에서 불러서 해석한 매칭결과입니다. 원래는 800MHz에서 찾은 매칭값이지만, 실제 라이브러리 소자를 넣으면 750MHz라는 엉뚱한 곳에서 매칭되고 있는 것을 알 수 있습니다. 이 현상은 주파수가 올라갈수록 점점 심해집니다.

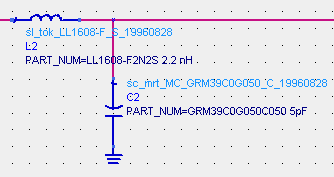
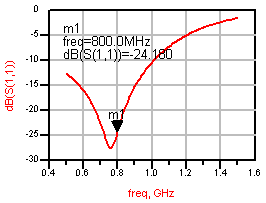
중요한 것은, 실제로 땜해서 만들면 왼쪽 그림이 아니라 오른쪽 그림과 같은 결과가 나온다는 것입니다. (라이브러리는 폼으로 있는게 아닙니다~) 그렇다면 원래 매칭주파수인 800MHz로 돌리기 위해서는 어쩔 수 없이 라이브러리의 소자값을 변화시켜 실제 매칭소자값을 찾아야 합니다. 아래는 800MHz에서 매칭이 가능하도록 하기 위해 라이브러리상의 소자값을 튜닝해가면서 찾아낸 '실제 매칭소자값'입니다.

이 예제에서는 직렬로 달린 인덕터의 값을 2.2nH에서 1.8nH의 라이브러리로 대치하자, 매칭주파수가 제자리로 돌아왔습니다. 보시다시피 원래 찾은 이상적인 LC값에서 크게 변하지는 않고 10~20% 정도 변한 값에서 실제 매칭소자값을 찾을 수 있습니다. 그렇기 때문에 처음에 스미스차트로 찾아낸 매칭값은 실제 활용가능한 값이 아니라, 튜닝을 위한 일종의 초기치로 감안하셔야 합니다. 그래서 처음 찾은 매칭값은 보통 seed라고 부르게 됩니다. 뭔가 자라내어 뽑아내기 위한 씨앗이란 것이죠.

그리고 라이브러리가 꼭 정확하리란 보장도 없습니다. 생산이 계속되다 보면 공정라인이 조금씩 변해서 소자의 특성도 좀 틀어질 수도 있습니다. 이 현샹은 주로 능동소자에서 심하게 발생하지만, 수동소자도 마찬가지입니다. 수동소자의 기생성분의 크기는, 공정시기는 물론 공정 lot에 따라서도 조금씩 달라지게 되는 등 여러 오차의 가능성을 내포하고 있습니다. 그러므로 결국 실제 소자를 붙여보고 조금씩 값을 바꾸어보는 튜닝이 필요할 수 있습니다.

그리고 또 한가지 더 허망한(?) 얘기를 하자면, 저렇게 찾은 값도 좀 부정확할 수도 있습니다. 왜냐하면 모든 수동소자값은 공정상에서 오차를 가집니다. 보통 5%, 10%, 20% 로 분류되어 판매되는데, 당연히 오차가 작은 소자종류가 더 비쌉니다. 결국 이말은 무엇을 의미하냐면, 우리가 10pF이라고 생각하고 붙인 소자가 9pF나 11pF같이 오차난 값이 될 수도 있다는 것입니다. 그래서 노련한 설계자라면 이정도 오차를 감안하여 초기 디자인을 하게 됩니다. 또는 설계가 다 끝난후 소자값의 오차가 아주 random하다는 가정하에 결과 트랜드를 보는 monte-carlo simulation을 수행하기도 합니다.

위의 사항들을 종합적으로 정리해보면 아래와 같습니다.

- 스미스차트로 찾은 LC값은 초기치이며, 실제 소자 라이브러리를 이용하면 결과가 달라진다
- 그것을 보정하기 위해 라이브러리 소자를 이용하여 소자값을 최적화하는 튜닝을 한다
- 실제로 회로에 장착해보고, 좀더 개선된 결과를 볼 수 있도록 핸드튜닝을 한다
- 소자값의 오차에 따라 결과가 어떻게 변하는지 예측해보고, 오차에 대한 민감도를 떨어뜨릴 수 있는
소자배치를 고려해본다 (쉽지 않은 일이므로 이것은 필수라기 보다는 권장사항임)

이렇듯 고주파 RF 설계는 결코 만만하지 않습니다. 완벽한 설계는 정말 쉽지 않은 일이며, 많은 부분 노가다가 필요하게 됩니다. 때로는 소자값 보정등에 대한 과정 없이 핸드튜닝만으로도 해결하기도 하지만, 어쨋든 이러한 제반 배경사항을 미리 알아둘 필요가 있습니다.

마이크로스트립 매칭의 마무리

LC 매칭이 저렇게 여러 오차를 극복해야 한다면, 마이크로 스트립 매칭은 어떨까요?
비슷한 문제들이 발생합니다. T.T

마이크로스립으로 50옴 선로를 만들어보신 분은 아시겠지만, 그냥 마이크로스트립 선로 계산기로 계산된 수치는 50옴에 딱 안떨어지게 됩니다. 단순히 대수적연산만으로는 잘 맞을 때도, 안맞을 때도 있어서 50옴으로 선로를 계산하고 에칭을 떠도 47옴이나 54옴 등 다른 값으로 측정되는 경우가 비일비재하지요. 패치안테나의 사이즈를 그냥 손으로만 계산해서 만들면 항상 중심주파수는 어디론가 시프트되는 것과 같습니다.

만약 그렇다면 이렇게 매칭선로를 계산하여 기판에 구현해도 그 매칭성능이 정확히 유지되고 있을까요? 물론 아닐 것입니다. 매칭도 틀어지게 됩니다. 그리고 역시 주파수가 올라갈수록 그 오차는 심해질 수 있습니다. 이런 일은 이론과 실제의 차이 및 기판조건에 따라 발생하는 문제입니다.

이것을 해결하기 위해서는 회로를 한번만 뜨는게 아니라 두 번 이상 떠봐야 할 것입니다. 처음에 한번떠서 그 오차의 방향을 계산하고, 그것을 감안하여 설계치를 조금씩 미리 보상하는 것이죠. 말이야 쉽지 참말로 귀찮은 일입니다.

그나마 이런 과정을 최소화 할 수 있는 길은 2.5D field simulator를 이용하는 것입니다. 선로만 따로 떼어내어 momentum, Ensemble, sonnet, IE3D 와 같은 평면회로 전용해석툴을 이용하면 단순히 회로적인 계산으로 구현된 해석결과보다 실제에 근접한 결과를 얻을 수 있습니다.

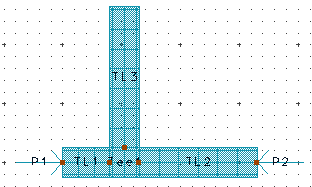
특히 아래와 같은 junction부분의 계산이 문제가 됩니다. 신호가 직각으로 교차하는 저런 부분은, schematic상에서 계산오차가 상대적으로 큰 편에 속합니다. 그래서 선로 전체를 해석하기엔 시간이 많이 걸리기 때문에 junction부분만 따로 떼어내어 해석 하는 경우가 많습니다.

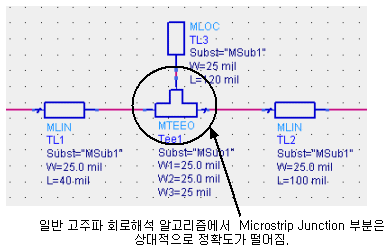
또한 부득이하게 스텁이나 선로를 휘게 만든 경우, 중심선의 길이를 일정하게 유지한다해도 꼬고나면 결과가 바뀌는 경우가 많아집니다. 이런 경우 역시 filed simulation의 도움을 받아서 꼬기 전의 결과랑 같은 결과를 내는 튜닝 길이를 찾아내면 실제와 많이 유사해집니다.

이렇듯 마이크로스트립을 정확하게 설계하고 싶다면, 필드 시뮬레이터의 도움을 받아야 하는 경우가 많아집니다. 마이크로 스트립은 그 특성상 일단 제작되면 튜닝이 무척 까다롭기 때문에, 가능하면 회로를 에칭해서 인쇄하기 전에 이처럼 실제랑 가장 유사하게 나올 수 있도록 최적화해놓을 필요가 있습니다.

LC 매칭과 마찬가지로 스미스차트를 통해 얻은 마이크로스트립 매칭선로값은 seed로 여기고, 어느정도 튜닝의 여지가 있다는 것은 유념해두시기 바랍니다.

안정원 보기 (Stability Circle)

스미스 차트를 통해 볼 수 있는 유용한 기능중의 하나가 바로 안정원(Stability circle)을 보는 기능입니다.

안정원이란 회로나 시스템의 발진여부를 판단하는 원으로서 주로 amp류의 설계에서 자주 보게 되며, 스미스차트상에서 아래와 같이 나타납니다.

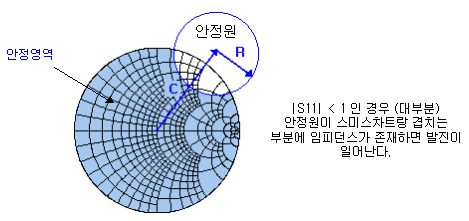
안정도계수 K가 1보다 크면 회로가 발진없이 안정하다는 의미이며, 이 경우 안정원은 스미스차트 밖으로 밀려나게 됩니다. 만약 안정원의 일부가 스미스차트와 겹치게 되서 그 겹친 영역에 회로의 임피던스가 존재하면 발진이 일어나게 됩니다.

여기서 안정원(stability circle)이란 용어는 그 원안에 들어가야 안정하다는 의미가 아니라, 안정하냐 불안정하느냐를 따지는 circle이라는 의미일 뿐이므로 혼동이 없으시길 바랍니다.

그래서 어떻게든 안정원을 밖으로 밀어내도록 회로를 구성하여 K가 늘 1보다 큰 unconditionally stable(무조건안정)을 이루도록 만드는 경우가 많습니다. 많은 시뮬레이터들은 안정원을 스미스차트와 함께 plot해 주는 기능을 갖고 있으며, 이것을 통해 발진을 잡게 됩니다.

또한 발진기의 경우라면 역으로 고의적인 발진을 일으켜야 하기 때문에, 다른 회로와는 반대로 발진이 일어나는 임피던스를 찾기 위해 안정도 원을 사용하게 됩니다.

(이부분은 발진 강의에서 좀더 자세히 설명됩니다)

스미스차트에서 각종 지표 읽기

스미스툴을 써오셧으면 아시겠지만, 각 점에 해당하는 각종 지표를 화면에서 바로바로 실시간으로 알려줍니다. 이것은 프로그램에서만 보여주는게 아니라, 사실은 스미스차트 종이 상에서도 읽을 수 있습니다. 편리한 스미스툴만 사용한다면 몰라도 되겠지만, 스미스차트의 이해를 돕기 위해 스미스차트 상에서 각종 지표를 읽는 법을 정리해보도록 하겠습니다.

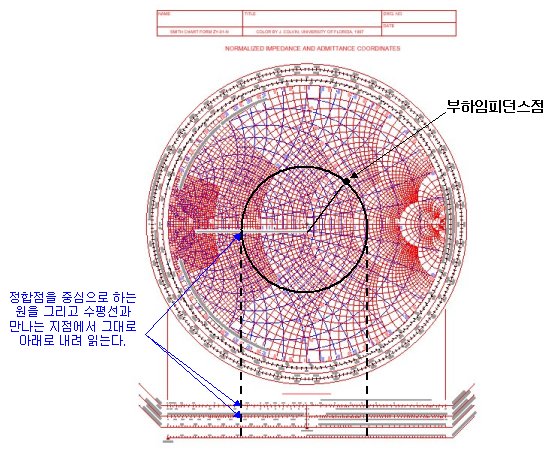
스미스 차트 원본에는 아래쪽에 길쭉한 도표가 하나 있는데, 그 도표는 위와 같이 해당 임피던스점의 반사계수 원과 허수임피던스가 0인 수평실수 좌표와의 만나는점에서 수직으로 그대~로 내려서읽습니다. 그 도표를 확대해보면 아래와 같습니다.

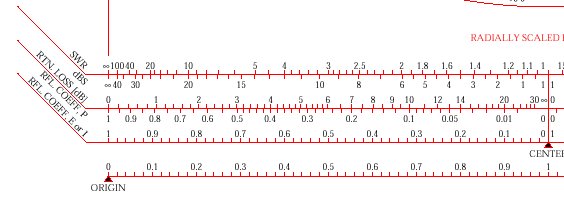
왼쪽 도표

오른쪽 도표

쉽지요? 그냥 읽기만 하면 SWR, Return loss, Reflection coefficient, Transmission coefficient 등 여러 가지 값을 바로 읽을 수 있습니다.

스미스차트는 편리해~

자! 드디어 스미스차트 기초강의가 마무리되었습니다. 스미스차트상의 각종의미와 읽는법, 임피던스 매칭법 등 종합적인 활용방법과 그 배경의 의미들을 돌아보는 기회가 되었으리라 생각됩니다.

마지막으로 다시한번 강조한다면, 스미스차트는 도구입니다. 사용법과 원리를 잘 배우고 쓰기 시작하면, 너무나 편리하고 유용한 도구입니다. 막연히 어렵게만 느끼셧던 분들이라 하더라도 이런 생각으로 접근하기 시작된다면, 조만간 스미스차트는 편안한 친구가 되어 있음을 알 수 있을 것입니다. ^^

<< Back