L, C 매칭은 계산식도 간단하고 비교적 쉽게 익혀집니다. 반면에 Microstrip과 같은 전송선로 매칭은 뭔가.. 뭔가 이상해서 처음에 좀 아리까리하기 마련이죠. 해보신 분은아시겠지만, 전송선로 매칭도 방법론은 그리 어렵지는 않습니다. 여기서는 LC 매칭과는 방법이 꽤 다른 전송선로 매칭, 그중에서 대표적으로 사용되는 전송선로인 마이크로스트립(microstrip)을 이용한 매칭방법을 들여다보고 그 속뜻을 풀어보도록 하겠습니다. LC매칭보다는 조금은 어려울 수 있으니 집중하여 학습하셔야 합니다.
![]() 직렬(series)
전송선로의 의미
직렬(series)
전송선로의 의미
전송선로 매칭을 하려면, 우선 매칭이 시작되는 부하임피던스점에서 선로를 길 게 한번 뽑고 시작합니다. 그렇다면 우선 이 직렬 선로의 의미부터 파악해보도록 하겠습니다.
전자회로 상식수준에서 직렬선로를 언뜻 생각해보면, 신호특성이 크게 바뀔 것이 없어 보입니다. 그냥 선로니까 신호를 전달할 뿐이겠죠. 맞습니다. 다만 고주파신호의 경우 어떤 것이 변화하게 될까요?
쉽게 답이 나오겠지만, 바로 위상이 변화합니다. 파장이 짧으니까 선로 길이에 따라 신호의 위상이 변할 것입니다. 그리고 이렇게 직렬선로를 뽑는다는 것은 스미스차트상에서 아래와 같은 궤적으로 표현됩니다.

현재 선로가 가진 자체 임피던스점을 중심으로 원형을 그리며 돌 게 됩니다. 그래서 스미스차트 맨 가생이를 잘 들여다보면, 위상지표가 파장길이로 표시되어 있는 것을 발견할 수 있지요.
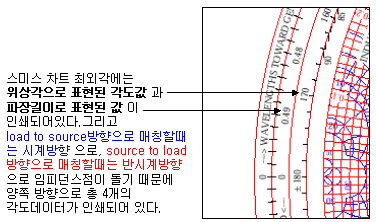
이렇게 임피던스점을 중심으로 반 바퀴 돌면, 90도(λ/4)만큼 진행한 것이 됩니다. 이것은 스미스차트 생성 수식자체에서 나오는 원리로서, 일단 사용자 입장에선 스미스차트에서 한 바퀴 도는 것은 180도 위상이 변한 것을 의미한다는 것을 잘 알아두어야 합니다.
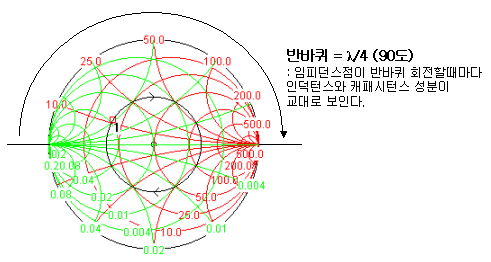
결국 선로를 길게 뽑으면 임피던스는 그대로 유지한채, 신호의 위상만 변화하게 되는 것이 됩니다. 마이크로스트립에선 결국 선로의 폭이 임피던스를 의미하므로 일정한 폭으로 길어진다는 것은 선로 임피던스가 유지되고 있다는 뜻이 됩니다. 스미스차트상에서 회전하면서 변한 것은 부하임피던스에서 보여지는 임피던스값이 변한 것일 뿐, 선로의 임피던스자체는 고정되어 있다는 점에 주목할 필요가 있습니다. 아래 그림에서 보여지듯이, 동일한 임피던스 선로상에서 진행되는 고주파신호의 크기는 변하지 않습니다. 선로 길이와 그 위치에 따라 위상이 변할 뿐입니다.
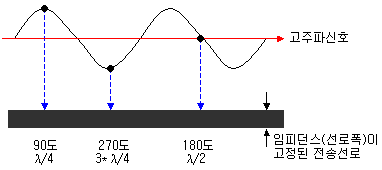
신호의 위상이 변한다는 의미를 좀더 풀어서 생각하면, 임피던스가 불일치해진 점에서의 반사계수 위상만 달라진다는 의미가 됩니다. 스미스차트상에서 임피던스점은, 동시에 반사계수를 의미한다는 것은 이미 잘 알고 계실 것입니다. 그리고 그 반사계수는, 중심점(50옴)에서 떨어진 반경을 의미하지요. 그래서 부하임피던스에서 50옴 선로를 길 게 뽑아봐야 반사계수의 크기는 변하지 않고, 단지 그 반사파의 위상관계만 변하는 것입니다.

즉 반경이 일정하게 원으로 돌기 때문에 반사되는 신호의 양은 변하지 않으면서, 반사파의 위상만 바뀐다는 의미가 되지요. 언뜻 생각해보아도 단지 선로만 길 게 뽑았는데 반사량이 줄어들 이유는 없겠지요?
그렇다면 만약, 50옴이 아닌 다른 선로폭으로 길 게 뽑으면 어떻게 될까요? 아래 그림과 같이 스미스차트 좌표상에서 해당 선로 임피던스 점을 중심으로 원을 그리며 돌 게 됩니다. 그리고 중심점이 어디건간에 부하임피던스점을 지나는 원주를 그리게 되기 때문에 아래처럼 임피던스에 따라 원의 크기가 달라집니다.
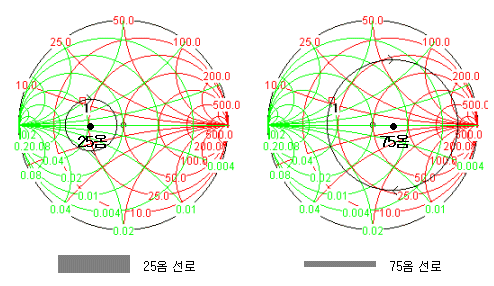
같은 부하임피던스 점을 이동시키더라도, 직렬로 뽑는 선로 임피던스를 어떤 값으로 뽑느냐에 따라 이동궤적을 다르게 선택할 수도 있다는 점이 중요합니다. 이것으로 부하임피던스점에서 선로를 길 게 뽑으면 임피던스가 어떤 궤적을 그리며 변하는지 알 수 있었습니다.
매칭을 할 때 이렇게 우선 선로를 한번 길 게 뽑는 이유는, 부하임피던스 점을 중심점으로 바로 보낼 수 있는 원 상에 올려놓기 위한 것입니다. LC 매칭에서 보셧듯이, 최종적으로 중심점에 갖다놓기 위해서는 어드미턴스 좌표계의 원중에서 중심점을 지나는 원에 먼저 올려놓아야 중심으로 보내는 궤적을 만들 수 있습니다. 전송선로 매칭 역시 우선 직렬선로를 뽑은후, 병렬선로를 통해 매칭을 완료하게 되므로 직렬선로를 뽑은 후에는 어드미턴스좌표계에 주목해야 하는 것입니다. 그렇게 되는 어드미턴스원은 Y=0.02가 되는 원이며, 이것은 Z=50옴 임피던스의 역수 1/50 을 의미합니다. (만약 normalize된 점으로 본다면 Y=1이 되는 좌표입니다만, 스미스툴은 normalize를 하지 않고 실제값을 그대로 쓰게 되어 있으므로 Y=0.02의 원으로 표현됩니다.)
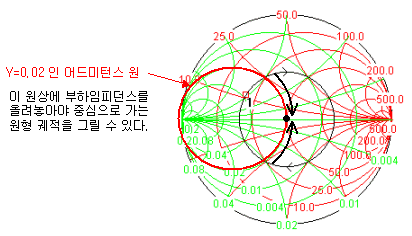
그리고 이러한 직렬 선로의 길이는, 아래의 그림에서처럼 스미스차트 맨 바깥쪽의 상대파장 (몇분의 λ)길이를 읽어서 그 차를 구하면 됩니다.
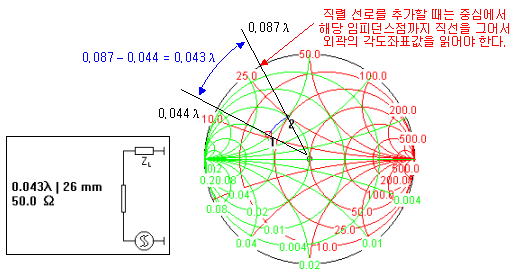
그런데 일반적인 LC 매칭이나 스텁의 계산에서는 허수임피던스좌표를 기준으로 하지만, 직렬 선로를 추가할 때는 중심에서 해당 임피던스점까지 직선을 그어서 최외각의 파장길이를 읽습니다. 왠지 헷갈리죠?
이것은 직렬선로가 특정 임피던스점을 목표로하는 것이 아니라 일정한 반사계수(반지름길이)를 유지하면서 위상차를 조정하기 위한 목적이 우선되기 때문입니다. LC소자와 스텁은 실제로 허수 임피던스 성분만 조정하는 역할을 하게 되지만, 직렬선로는 그 특성상 반사계수의 크기를 유지한 형태로 위상만 변합니다. 그래서 직렬선로를 추가하면 실수와 허수 임피던스 둘다 변하게 되며, 반사계수궤적을 기준으로 하기 때문에 임피던스점을 읽지 않고, 반사계수의 위상변화를 기준으로 한 상대파장 좌표를 읽게 되는 것이지요. 조금 어렵게 들리는 얘기이겠지만, 사실은 스미스툴을 이용하는 경우는 그냥 돌리기만 하면 친절하게 바로 계산해주기 때문에 그냥 넘어갈 수도 있습니다. 그래도 원래 계산하는 방법론이 이렇다는 것을 잘 알아두어서 손해볼 리는 없겠지요? ^^
만약 50옴이 아닌 선로로 길 게 뽑는다해도, 똑같이 어드미턴스=0.02 인 원에 임피던스를 이동시킬 수 있습니다. 그렇기 때문에 전송선로로 매칭할 때는 전송선로의 폭과 길이가 동시에 결정되어야 합니다. LC매칭에서는 한단한단 매칭할 때 단지 해당되는 L, C 값만 찾으면 되지만, 전송선로 매칭은 LC매칭보다 두배의 변수가 존재하게 되는 셈입니다. 이것은 선택의 폭이 넓다는 장점도 되지만, 한편으로는 결정해야 될 게 많아서 귀찮은 문제이기도 한 것이죠.
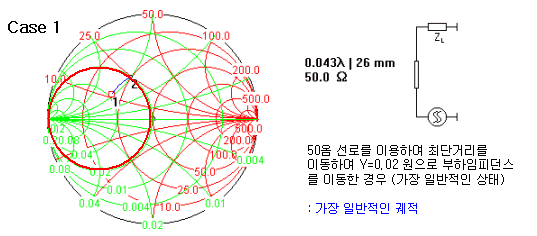
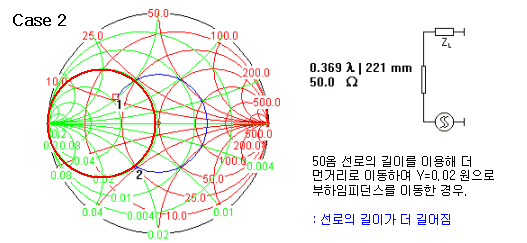
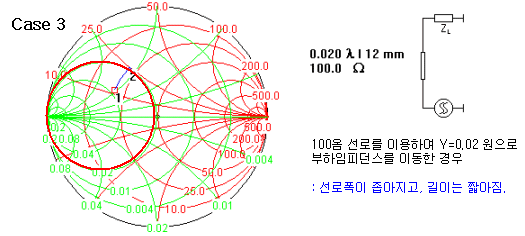
위 그림에 나와있듯이, 똑같이 어드미턴스=0.02 인 원에 부하임피던스를 올려놓는데는 여러 가지 길이와 폭이 존재합니다. 그러므로 상황에 맞게 원하는 모양새로 직렬 선로를 뽑아야 하는데, 일반적으로 특별한 이유가 없는 한은 그냥 50옴 폭의 선로를 이용하여 최대한 짧은 길이값으로 결정하는 경우가 많습니다. 50옴으로 하는게 계산이 편리해서이지만, 상황에 따라 선로길이를 바꾸어야 할 때는 임피던스도 바꾸어가면서 같은 궤적을 그리도록 하는 것도 각자 판단해야 할 테크닉입니다.
![]() 병렬
스텁 (Shunt stub) 달기
병렬
스텁 (Shunt stub) 달기
이제 직렬전송선을 뽑아서 부하임피던스점을 어드미턴스=0.02 인 점에 올려놓았으니, 그것을 돌려서 중심에 갖다놓아야 합니다. 직렬선로를 하나 뽑았으니 이제 병렬 선로를 뽑을 차례인데, 이렇게 매칭을 위해 옆으로 길 게 뽑은 선로를 우리는 스텁(stub)이라고 부릅니다.
이 스텁은 마치 병렬 L,C 소자처럼 작동하는데, 스텁을 달았을 때의 스미스툴상의 궤적은 아래와 같이 마지막 부하임피던스점이 위치한 어드미턴스 원 상을 뺑뺑 도는 궤적을 그리게 됩니다.
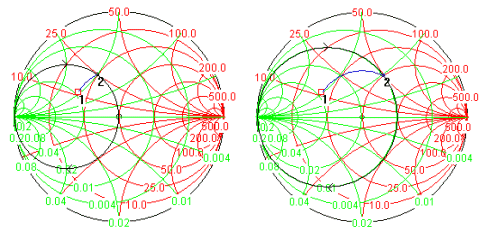
그런데 종이와 콤파스를 이용한 고전적인 스텁매칭을 할 때와 궤적을 그리는 방식이 다르다는 것을 눈치채신 분들이 계실 것입니다. 위의 궤적은 실제로 스텁에 따른 계산 거리를 산출하기 위한 궤적이 아니라, 스미스툴상에서 개념적으로 임피던스점을 이동하기 쉽게 하기 위해 계산된 별도의 궤적입니다. (이 문제는 더 아래쪽에서 알아보기로 하게습니다) 하여튼 스텁을 달면 위 그림과 같이 되기 때문에 부하임피던스를 중심점에 보내려면, 왼쪽 그림과 같이 어드미턴스=0.02 인 원상으로 임피던스점을 이동시켜놔야 하고, 결국 그것을 위해 바로 직렬 선로를 추가하게 됩니다. 이제 그 직렬 선로와 병렬 스텁의 연관관계가 눈에 보이기 시작하지요?
스텁을 활용하기 위해 우리는 중요한 개념하나를 짚고 넘어가야 합니다. 스텁에는 두가지 종류가 있는데, 바로 open stub과 short stub입니다. 마이크로스트립에서 오픈스텁은 그냥 신호선을 옆으로 딴 모양이고, 숏스텁은 그 스텁 끝단 바닥에 via를 뚫어서 밑면의 Ground와 연결시켜 Short 시킨 모양입니다.
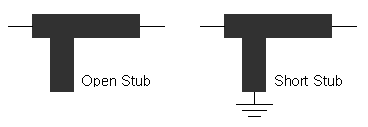
오픈 스텁과 숏 스텁의 차이는 언뜻 보면, 마치 인덕터와 캐패시터의 관계를 연상시킵니다. 그림으로 본다면 오픈 스텁은 신호선과 GND 사이에 넓은 판을 추가하여 마치 개념적으로는 병렬 캐패시터를 붙인 것처럼 되고, 숏 스텁은 병렬 인덕터를 붙인 것처럼 됩니다.
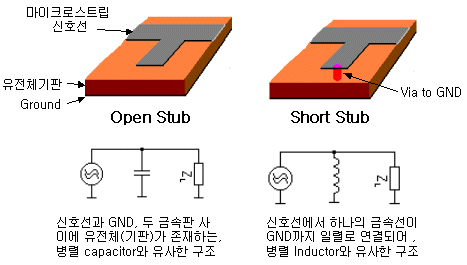
그래서 스미스툴상에서 오픈스텁과 숏 스텁은 정반대의 궤적 방향을 그리게 됩니다.

LC매칭의 경우를 아시겠지만, 어드미턴스
원상에서 반시계방향으로 도는 것이 병렬 인덕터, 시계방향으로
도는 궤적이 바로 병렬 캐패시터를 의미하지요! 그래서 대부분의 매칭
지역에서 위로 올라가는 궤적은 인덕터, 내려가는 궤적은 캐패시터라는
LC매칭의 공식과 전송선로매칭의 공식이 같아집니다.
신기하죠?
^^
다만 스텁의 경우는 소자와는 달라서, 원을 타고 돌 때마다 해당 스텁이 실제로 인덕턴스 성분으로 보이느냐 캐패시턴스 성분으로 보이느냐가 바뀝니다. 왜냐구요? 빙빙 돌고 있으니까요~!
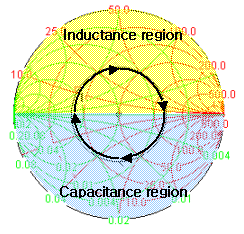
이것은 lumped elment 인덕터/캐패시터가 특정 위치(SRF)를 넘어서면서 L과 C의 역할이 뒤바뀌는 원리와 유사합니다. 인덕터건 캐패시터건 reactance 소자들은 두 개의 성분을 동시에 갖고 있고, 상황에 따라 어느 것이 더 주요하게 나타나는지가 결정되는 것이니까요.
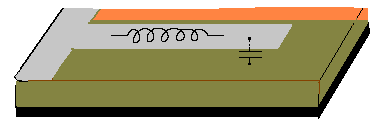
아래는 마이크로스트립으로 만들어진 스텁이 어떤 reactance 성분을 가지는지를 등가회로로 간략히 표현한 그림입니다. 선로 그자체의 길이로 만들어진 인덕턴스와, 그 스텁선로와 GND판 사이에 유전체 기판이 존재함으로써 자연적인 캐패시턴스가 존재하게 됩니다. 즉 하나의 스텁은 이 두가지 성분을 다 가지고 있으며, L과 C 성분은 서로 반대적 성향을 갖고 있어서 그 길이에 따라 두 성분중 어느것이 dominant해지느냐가 결정되는 것이지요.
오픈 스텁의 경우는 처음엔 병렬 캐패시터처럼 보이지만, 어느 길이 이상이되면 선로자체가 길어지면서 인덕턴스 성분이 주요하게 되어 인덕터처럼 보이게 됩니다. 또 그 길이가 어느 이상을 넘어서면 다시 캐패시턴스 성분이 주요해져서 캐피시터 처럼 보이게 되구요. 스미스차트 원을 반바퀴 돌 때마다 인덕턴스와 캐패시턴스 성분이 서로 교차되며 보이는 것입니다. (직렬선로 추가의 경우와도 동일합니다.)
다시 본론으로 돌아가서, 사실 위와 같은 인덕턴스/캐패시턴스 변화에 대한 이론과 실제는 하나도 몰라도 매칭이 가능합니다. 스미스차트상에서 단지 임피던스를 중앙에 올려놓을 수 있는 스텁의 길이만 찾으면 땡이니까요. 그렇지만 위와 같은 원리를 잘 곱씹어 보아야 개념을 잡을 수 있습니다.
여하튼 스텁길이를 찾는 과정은 병렬 LC매칭을 구현할 때와 마찬가지로, 허수 어드미턴스 좌표계를 읽고 그에 해당하는 파장차이를 읽으면 됩니다. 그리고 그것이 오픈스텁이냐 숏스텁이냐에 따라 회전하는 거리가 달라집니다. 아래 그림을 보시지요!
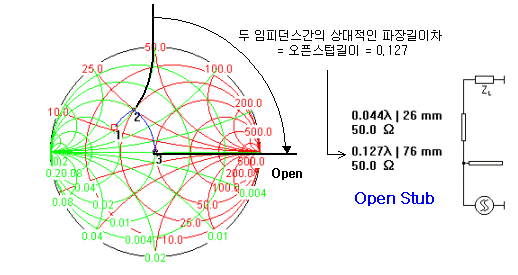

오픈스텁의 경우 해당 임피던스 허수좌표점에서 오른쪽 원끝까지 돌리고, 숏스텁의 경우는 왼쪽 끝까지 도달하도록 돌립니다. 그리고 이동한 만큼의 허수좌표계상의 상대파장길이를 구하면 그것이 스텁의 길이가 됩니다. 위에서 화살표로 나타낸 궤적 이동법은 저 위에서 언급한, 종이와 컴파스를 이용한 고전적인 스텁길이 계산에 사용되는 궤적입니다. 스미스툴에서는 사용자의 직관적인 이해를 돕기 위해 파란색 원으로 나타내지만, 원래 계산법은 위와 같은 회전을 통한 파장거리를 계산한다는 점은 알아두시기 바랍니다.
같은 매칭을 하는 경우 오픈스텁이건 숏 스텁이건 똑같이 매칭할 수 있지만, 보시다시피 그 길이가 달라집니다. 눈치를 채신분은 아시겠지만 숏스텁과 오픈스텁은 스미스차트 반 바퀴, 즉 λ/4파장만큼 길이가 다릅니다. 매칭시켜야 하는 임피던스점이 스미스차트 위쪽에 있으면 오픈스텁이 더 짧고, 아래쪽에 있으면 숏스텁으로 매칭하는게 거리가 짧아집니다. 그래서 최단 길이에 맞는 스텁을 골라서 결정하면 됩니다만, 실제로는 거의 오픈 스텁을 사용하게 됩니다. 숏 스텁은 마이크로 스트립 기판을 뚤고 via를 박아서 위와 아래 금속을 연결해야 하는데, 이 공정은 돈도 많이 들고 구현하기도 그리 수월치 않으며, 고주파가 될수록 via 위치에 따른 특성변화를 정확히 잡아내기 힘들기 때문입니다. 오픈 스텁을 쓰면 복잡한 via 공정 없이 그냥 인쇄만 하면 되기 때문에, 실제 숏스텁은 잘 쓰기기 힘듭니다.
스텁을 달 게 될 때, 한가지 더 고려해야 될 사안이 있습니다. 직렬선로와 마찬가지로 스텁의 임피던스 값(선로폭)을 어떤 값을 사용하느냐입니다. 우선 스텁의 임피던스가 다를 때 궤적의 변화는 어떠한지 아래 그림을 참조해보시지요.
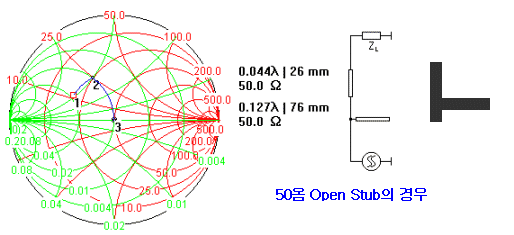
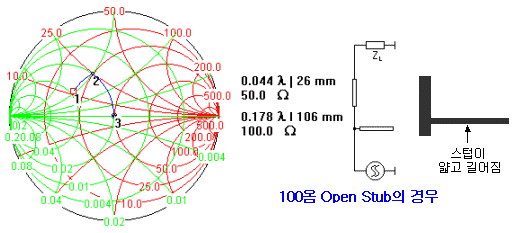
스텁의 임피던스가 다를 때는, 이상하게도 스미스툴상의 궤적만 봐서는 모양이나 방향에 전혀 변화가 없어보입니다. 스텁의 임피던스가 변할 때는 궤적의 형상이나 위치가 변하는게 아니라, 궤적간의 이동거리에 따른 선로의 상대파장길이값이 변화합니다. 위에서 50옴과 100옴 오픈스텁을 이용하여 매칭한 결과를 보시면 알겠지만, 스텁의 임피던스를 높이면(폭을 좁히면) 길어집니다. 이것은 결국 병렬 capacitor의 역할과 비슷한 오픈스텁이, 그 선로폭이 좁아지면서 동일한 캐패시턴스 면적값을 가지기 위해 길이가 길어진 것으로 볼 수도 있습니다. 이 말의 의미를 한번 찬찬히 생각해보시길 바랍니다. ^^
자, 이로서 부하임피던스를 중심에 갖다놓는데 성공했습니다. LC매칭보다 설명이 꽤 복잡해보이는데, 보시다시피 방법론 자체는 별 것 아닙니다. 많은 경우 전송선로 매칭은 그 방법을 정확히 익힌 후, 역으로 이론을 이해하는게 더 빠른 경우가 많습니다.
![]() 정리
: 마이크로 스트립 매칭
정리
: 마이크로 스트립 매칭
자세히 언급하느라 설명이 길었는데, 이러한 전송선로 매칭법을 마이크로스트립으로 구현할 때 그 과정을 요약해보도록 하겠습니다. 아래 예제는 LC 매칭 예제에 사용된 것과 마찬가지로, 부하 임피던스 20+j12 점을 500MHz를 중심주파수로 50옴에 매칭시키는 예제입니다.
1. 부하임피던스점에 직렬선로를 추가하여, 임피던스점을 어드미턴스=1인 원에 이동시킵니다. 그리고 그때의 선로길이를 구하되, 특별한 경우가 아니면 일단 선로 임피던스는 50옴으로 사용합니다.
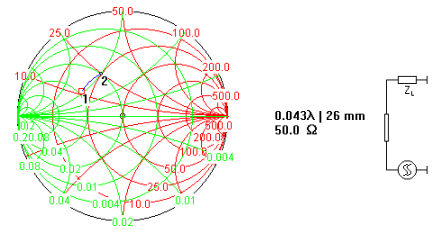
2. 이제 오픈스텁을 추가하여 어드미턴스=1 원상에 올라간 임피던스를 그대로 돌려서 50옴 중심점에 매칭시킵니다. 그리고 그 길이를 구하되, 역시 특별한 이유가 없다면 선로폭은 50옴으로 고정합니다.
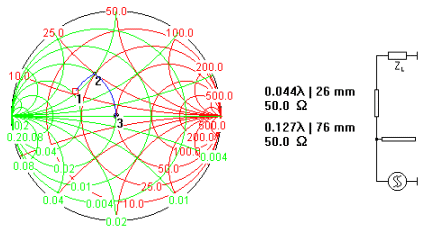
3. 계산된 매칭선로들의 파장 길이를
마이크로 스트립 기판의 관내파장으로 적용하여 실제 선로 길이를 구합니다.
(유전율=4, 높이가 1 mm 인 마이크로스트립 기판을 사용한 경우)
*
스미스툴을 이용하면 파장길이와 함께 공기중의파장길이가 자동으로
계산됩니다
계산된
직렬선로 길이 : 0.044 * λ = 26mm (공기중의 파장길이)
계산된
스텁 길이 : 0.127 * λ =76mm (공기중의 파장길이)
실제 길이를 구하려면 공기중의 파장 길이를 관내파장 길이로 바꾸어주어야 한다.
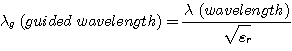
|
실제
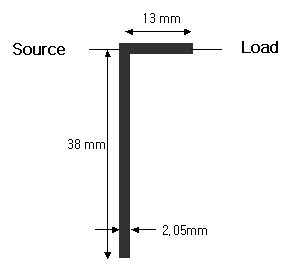
직렬 선로의 길이 : 26mm / 2 = 13mm |
4. 역시 마이크로스트립 기판정보에 맞추어
해당 임피던스에 해당하는 선폭을 구합니다.
(3,4번은 순서가 바뀌어도
무관함)
임피던스에 따른 실제
선폭 계산 및 계산툴은 이곳을 참조 -> 마이크로스트립이란?
현재기판상에서
계산된 실제 50옴 선로의 선폭 = 2.05mm
5. 완성되었심다! 예제회로의 주파수가 낮아서 선로들이 꽤 깁니다.
![]() 특별한
경우 - 매칭선로 길이 조정하기
특별한
경우 - 매칭선로 길이 조정하기
지금까지 알아본 방법은, 마이크로스트립 매칭의 아주 기본적인 흐름입니다. 이제 위에서 열거되었던 스미스차트상 특성과 이론을 이용하여 좀더 고단수의 매칭테크닉을 들여다 보도록 하겠습니다.
실제로 위와 같은 방법만으로도 매칭하는 것 자체에는 아~무~런 지장은 없습니다. 그런데 살다보면 별의 별 일이 다 발생하지요. 저렇게 계산된 선로들을 계산하다보면 알 수 없는 걸림돌들이 발생하기도 하는데, 매칭값으로 계산된 선로가 너무 짧은 나머지 구현이 애매한 경우가 있습니다. 또한 레이아웃을 하다보면 공간배치상 어쩔 수 없이 스텁이 들어갈 자리가 모자르거나, 남는 공간에 교묘하게 깔아야 하는 당혹스런 경우가 발생하기도 합니다.
이럴 때, 전송선로 매칭의 원리들을 잘 상기해보면 여러 가지 해결법이 존재합니다.
1. 선로 임피던스를 조절한다.
가장 유용하고 간편한 방법중 하나입니다. 위의 설명들에도 나와있지만, 임피던스를 상황에 맞게 늘이거나 줄임으로써, 즉 폭을 조절함으로써 길이도 조정할 수 있습니다. 때에 맞게 적절히 활용할 필요가 있습니다.
2. λ/2 만큼의 선로 길이를 더한다.
그냥 반파장의 길이를 더해 버리면 스미스차트를 한 바퀴 돌아 버린 셈이 되므로 똑같은 매칭효과를 기대할 수 있습니다. 물론 공간적으로 그리 효율적인 방법은 아니지만 궁여지책으로 사용해볼만 합니다.
3. 오픈 스텁과 숏스텁중 적절한 길이의 놈으로 선택한다.
같은 매칭이라도 오픈 스텁일 때와 숏스텁일때랑 길이가 다릅니다. 숏스텁을 쓰는데 별 지장이 없는 상황이라면 시도해볼 가치는 있습니다.
4. 꺾는다.
어찌보면 가장 흔히 사용하는 방법중의 하나입니다. 중심선의 길이를 유지한채 꺾는 것입니다. 그러나 이 꺾임으로 인해 실제 길이 특성이 변하는 경우가 많습니다. 특히 주파수가 올라갈수록 심해지므로, 가능하면 EM simulation 등을 통해 보다 정확하게 꺾은 길이를 튜닝할 필요가 있습니다.

5. 스텁대신 Lumped 소자를 사용한다.
LC매칭때를 잘 생각해보시면, 어드미턴스=1인 원에 올라간 점을 중심으로 옮기는데는 꼭 스텁이 아니더라도 병렬 캐패시터/인덕터 소자를 통해서도 가능하다는 것을 기억하실 것입니다. 당연히 실제로도 구현 가능합니다. 스텁대신에 병렬 캐패시터를 이용하여 붙이면 큰 스텁을 확 줄여 버릴 수도 있습니다.

다만 이 방법은 소자특성상 고주파에선 적용하기 힘들고, 적당히 낮은 주파수에서 사용가능합니다. 또한 MMIC의 경우에는수십GHz에서도 칩 내에서 MIM 캐패시터를 이용할 수 있으므로 이런 방법을 종종 사용하기도 합니다. 잘 활용하면 괜찮은 방법이지요.
6. 다단 매칭을 한다.
직렬선로와 스텁 하나로 매칭하지 않고, 스텁을 두 개 이상 달아서 매칭하면 나름대로 길이와 dimension들을 조정할 수 있습니다. 스미스차트에서 임피던스점을 이리저리 돌려가면서 적절한 길이가 나오는 궤적을 만듦으로써 구현되며, 회로의 Q값을 낮추어 광대역으로 매칭하기 위해서도 사용됩니다.
|
|
이 모든 방법은 원리적인 면에서 들여다보면 쉽게 이해할 수 있는 방법들입니다. 단순히 방법만 배우기보다는, 적어도 왜 그렇게 되는지 이해하는 것은 내공을 강화하여 고수가 되기 위한 중요한 수련과정일 것입니다.
![]() 50옴
선로의 길이
50옴
선로의 길이
임피던스 매칭을 마무리하기 하기위해, 한가지 짚고 넘어가 볼 게 있습니다. 직렬선로상에선 반사계수가 변하지 않고, 단지 신호반사에 의한 위상만이 변화한다는 것을 배웠습니다. 그렇다면, 우리가 Jig를 만들거나 특별한 의미없이 신호를 전달하기 위해 연결하게 되는 50옴 전송선로는 어떨까요?
초보시절에 이런 의문을 가지시는 분들이 많이 보았습니다. 매칭을 위해 직렬선로를 살짝만 뽑아도 부하 임피던스가 휙휙, 돌아가는데, 그렇다면 그냥 매칭이 아닌 연결만을 위해 선로를 뽑았을 때는 과연 괜찮은 것인지??? 이런 경우 임피던스 관계는 어떻게 파악해야 하는가에 대한 문제입니다. 즉 매칭은 다 끝났고, 그냥 소자나 회로들을 연결하기 위해 선로를 깔아도 특성에는 변화가 없느냐는 문제이지요.

결론부터 말씀드리면, 그냥 연결선로로 사용된 50옴선로의 길이는 이론적으로 아무 문제가 없습니다. 실제로는 약간 loss가 부가될 수 있지만, 그리 크지 않게 그냥 신호를 깨끗하게 전송해줍니다. 왜일까요?
스미스차트 상에서 부하임피던스가 변한단는 것은, 그 부하임피던스점에서 본게 아니라 소스쪽에서 본 임피던스로 생각할 수 있습니다. 즉 매칭의 목적지가 되는 50옴에서 볼 때 저 멀리 끝단까지 포함한 임피던스가 어떻게 보이느냐의 문제인 것이죠. 그러므로 매칭이 이미 끝나서 앞뒷단이 모두 50옴의 신호 흐름에 최적화되어 있다면, 그것을 스미스차트에서 확인하면 아래와 같이 됩니다.
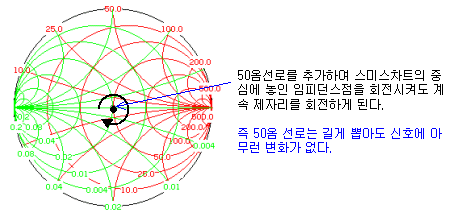
다시 말해 이미 50옴과 50옴으로 임피던스가 잘 통일된 단끼리 선로를 연결하면, 그 선로가 아무리 길어져도 스미스 차트 중심에서 뱅뱅 돌기 때문에 반사계수의 위상 역시 변할 이유가 없습니다. 매칭이 안되어서 한쪽 임피던스가 중심이 아닌곳에 붕 떠있을 때만 선로 길이에 따라 반대쪽 임피던스가 변하는 것처럼, 선로 길이만큼 원을 그리며 돌 게 되는 것이죠.
이 문제는 조금 어렵게 느껴질 수도 있지만, 같은 문제를 고민해보신 적이 있는 분들이라면 이게 무엇을 의미하는지 아실 수 있으리라 생각됩니다. 결국 이 얘기는 50옴과 같이 회로들을 동일한 특성 임피던스로 매칭(통일)시키는 이유이기도 합니다. 같은 특성임피던스로 연결단이 통일되어야지만 연결선로의 조건에 따라 임피던스 변화가 없고, 결국 신호 흐름에 변화가 일어나지 않기 때문이지요.
![]() 마치며
마치며
스미스차트를 이용한 매칭방법은 이론보다는 사용법을 배우고 이론을 이해할 필요가 있습니다. 그렇다고 사용법만 익힌다면, 그것은 반쪽의 배움이 될 것입니다. 스미스차트를 이용한 매칭강의를 계속 보신 분이라면 느끼셧겠지만, 매우 원리적인 방법으로 해결됩니다. 그러므로 스미스차트 궤적의 이동과 그것들의 의미를 곰곰히 생각해봄으로써, 누가 알려주지 않아도 자신만의 테크닉을 만들 수도 있습니다.
스미스툴과 같은 유용한 툴을 이용함으로써, 매칭과정의 노가다를 많이 줄이고 보다 명확하게 임피던스 매칭을 이해할 수 있도록 많은 연습을 하실 수 있기를 바랍니다.
Copyright by RF designhouse. All rights reserved.