스미스차트가 도구라면, 이제 그 도구의 사용법을 알아보도록 하겠습니다. 우선 스미스차트의 구조와 그 위에 찍힌 점을 어떻게 읽을 수 있는 것인지 알아보도록 하겠습니다.
![]() Normalization
(정규화)
Normalization
(정규화)
우선, 스미스 차트를 이용하기 위해 먼저 알아야 할 것이 바로 normalize에 대한 것입니다.
스미스차트 좌표상의 점이 의미하는 것은 임피던스라는 것은 이미 잘 알고 계실 것입니다. 이미 스미스차트를 사용해보신 분은 아시겠지만, 그 좌표를 찍기 전에, 먼저 어떤 정규화 과정이 하나 있다는 것을 기억하시죠?
바로 해당 임피던스 값을 특성 임피던스(Characteristic Impedance)로 나누어주는 것입니다. 일반적으로 우리는 이 특성임피던스 값을 50옴을 사용하는데, 우선 스미스차트 좌표상에 올리기 전에 50으로 나누고 나서 그 값을 올리게 됩니다. 예를 들어 70 + j12 에 해당하는 임피던스를 스미스차트 상에 찍어볼려면 50으로 나눈 1.4 + j 0.24 에 해당하는 좌표값에 점을 콕 찍게 됩니다. 왜일까요???
그것은, 특성임피던스가 꼭 50옴이지는 않기 때문입니다. 상황에 따라 75옴이 될 수도 있고, 또 어떤 특정 임피던스를 사용할지, 또는 아예 임의의 임피던스값을 잡던 사용자 맘대로 하기 위해서는 normalize를 해야 합니다.
이점을 이해하기 위해 우선 알아두어야 할 것은, 스미스차트의 중심점이 곧 특성임피던스를 의미하게 된다는 것입니다. 스미스 차트 중심점의 좌표는 1+j0 이기 때문이죠. 50+j0 옴의 특성 임피던스를 normalize하면 바로 1+j0입니다.
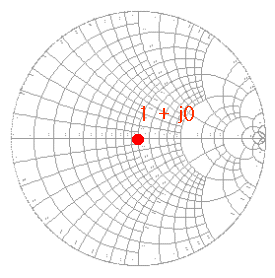
스미스차트 좌표는 어떤 특성임피던스에서도 동일하게 적용할 수 있으려면, 중심점이 50, 66, 75와 같은 어떤 특정한 하나의 임피던스좌표를 지칭해서는 안되겠죠. 그래서 스미스차트는 1이라는 임피던스 점을 기준으로 만들어놓고, 해당 임피던스점들을 각각의 회로와 시스템 특성에 맞는 임피던스로 나누어 쓰게 하는 것입니다. 결국 이것도 편하자고 이러는 것입니다.
![]() 스미스
차트에 점찍기
스미스
차트에 점찍기
기초부터 시작하는 마음으로.. 스미스 차트 상에 점을 찍으려면 우선 스미스차트 좌표의 구조와 특성부터 이해해야겠죠. 먼저 복소 임피던스를 찍으려면 실수좌표계와 허수좌표계를 이해해야 할 것입니다.
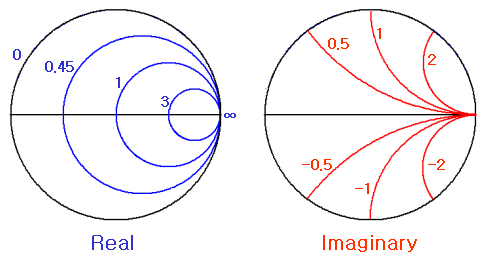
흠~ 뭐 좌표계가 좀 야리꾸리하게 생기긴
했지만 한두 번 점찍어보면 별거 아닙니다.
실수부는 수평선을 따라
오른쪽 끝이 무한 대의 중심점이 되고, 왼쪽으로 중심이 이동할수록
점점 값이 작아집니다. 즉 임피던스 점이 위치하는 곳을 지나는 원의
좌표값이 실수부 좌표가 되지요. 허수부의 경우는 오른쪽 끝을 기준으로
점점 퍼져나가는 포물선 형상이며, 위쪽은 + 부호로, 아래쪽은 - 부호의
좌표로 정의됩니다.
그런데.. 그런데 아예
초보인 경우라면 이런 의문마저 들 수 있을 겁니다.
" 점찍으라니 찍겠는데, 대체 뭔 임피던스를 찍으란 말이여?? "
그렇습니다. 도대체 무슨 임피던스를 찍어보란 말일까요? 아무 임피던스나 콱 찍으면 되는 건지??
그것은 어떤 용도로 스미스차트를 사용하느냐에 따라 다를 수 있습니다. 소자의 특성을 보는 경우라면 그냥 그 소자의 임피던스를 찍으면 되고, 임피던스 매칭을 하는 경우는 특성임피던스와 매칭시키고자 하는 부하(load) 임피던스를 찍습니다. 이 문제는 이 강의시리즈를 천천히 따라해가다보면 자연스럽게 이해될 것입니다.
그리고 스미스차트상에 점을 찍은 순간, 그 점은 임피던스를 나타냄과 동시에 반사계수를 나타냅니다. 이전 장에서 보았듯이, 스미스차트 자체가 반사계수와 임피던스관계를 통해 만들어진 좌표계이기 때문이죠. 그냥 좌표를 읽으면 그건 임피던스 점을 의미하고, 그 임피던스점까지 중심에서 떨어진 거리를 전체 반지름으로 나눈 값이 반사계수의 magnitude가 되고, 임피던스 점까지의 각도값을 읽으면 반사계수의 phase가 됩니다.
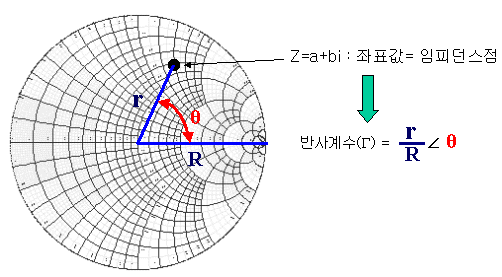
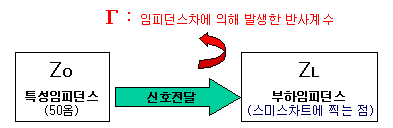
스미스차트 좌표상에서 임피던스 점은 곧 반사계수를 의미한다는 것은 이제 여러번 들어서 귀가 간지러우실텐데.. 여기서 한가지 고백할 점이 있습니다. 사실은, 임피던스 점을 가져와서 스미스차트에 직접 찍는 경우는 그리 많지 않다는 점입니다. 좌표계를 쉽게 이해하기 위해서 그렇게 설명한 것일뿐, 실제로는 반사계수를 스미스차트상에서 그대로 plot하여 역으로 임피던스를 알아내는 경우가 더 많습니다.
왜냐하면 RF에서 가장 흔히 사용하는 지표인 S파라미터를 그대로 갖다 쓰기 때문입니다. S11이나 S22 와같은 반사계수 지표를 스미스차트상에 나타내면 그게 바로 해당 부하 임피던스를 알려줍니다.
![]() 스미스
차트 점 들여다보기
스미스
차트 점 들여다보기
많은 경우, S11이나 S22 등의 반사계수들은 한주파수에서만 보는게 아니라 여러 주파수범위에 걸쳐 보게 될 것입니다. 그래서 그리다 보면 아래와 같은 식의 돼지 꼬리 그림이 나오기도 합니다.
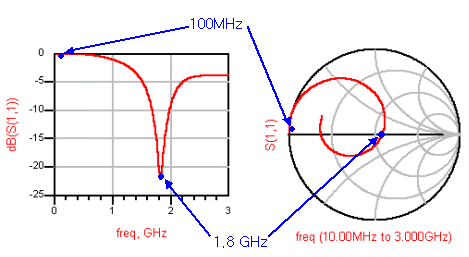
초보시절에는 스미스차트상에 하나의 점이 표시되지 않고 저렇게 줄줄히 꽈리를 틀면 대체 저게 뭔가.. 싶을 것입니다. 별거 아닙니다. 그냥 주파수별로 반사계수들을 줄줄히 보여준건데, 각 점마다 어느 주파수에서의 반사계수인지 쓰기가 지저분해서 안쓴 것일 뿐입니다.
그렇다면 저렇게 주파수에 따라 다르게 찍힌 점들을 해독하는 능력이 필요하겠죠? 여기서 복소임피던스 수식을 재탕삼탕해보겠습니다.
![]()
허수부의 +값은 인덕턴스(L)를, -값은 캐패시턴스(C)를 의하므로, 결국 스미스차트의 그림은 아래와 같은 의미로 표현됩니다.
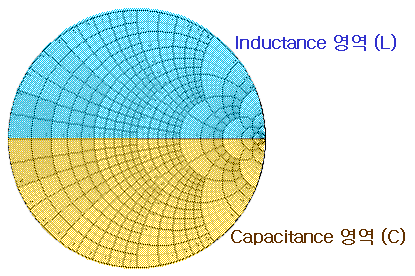
그래서 S11이 어느점에 존재하느냐는 결국 그 자체만으로 현재 부하임피던스가 인덕턴스 성분을 갖고 있는지, 캐패시턴스 성분을 갖고 있는지 쉽게 알 수 있습니다. 보는 즉시 바로바로 팍팍 감이 오지요!
또한 그것이 주파수별로 나타날 때, S11 궤적이 위와 아래를 걸치게 된다는 것은, S파라미터 플롯상에서는 어떤 극점을 가진다는 의미가 됩니다. 쉽게 말해서 올라가다가 내려가던지 내려가다가 올라가던지 하는 위치가 된다는 것이지요. 스미스 차트의 수평선을 통과하는 점에서는 기울기의 음양이 바뀌는 극점이 됩니다. 아래 그림을 참조하세요.
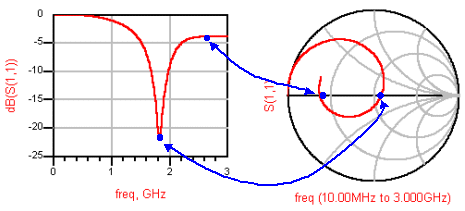
또한 임피던스점=반사계수의 원리에 의해 S11이 낮을수록 (즉 반사가 적을수록) 스미스차트상의 점들은 중앙부에 모이고, S11이 높을수록(반사가 많이 될수록) 중앙에서 멀어지고 흩어집니다.
아래는 Filter의 S파라미터를 plot한 것으로서, S11이 떨어지는 통과대역 주파수의 임피던스점들은 스미스차트에서 중앙부에 위치하고 있음을 알 수 있습니다. 임피던스 점의 반사계수 읽는 법에서 알 수 있듯이, 중앙부에 가까울수록 반사계수가 작다는 의미이므로 당연한 것이지요.
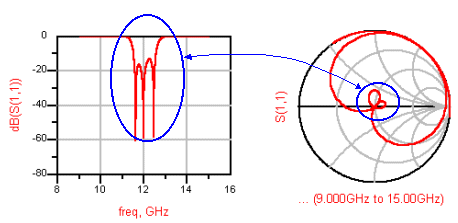
이러한 판독법들은 그냥 스미스차트 좌표계를 정확히 이해하면 자연스럽게 유도되는 것이지만, 많은 경우 경험적으로 익히는 경우가 더 많을 것입니다. 왜냐면 이렇게 설명한 책은 거의 없기 때문이지요. 차근차근 이해해보면서 스미스차트상의 점이 무얼 의미하는지 음미해보시기 바랍니다.
![]() 임피던스와
어드미턴스
임피던스와
어드미턴스
지금까지는 임피던스의 관점에서만 스미스차트를 설명했습니다. 그런데, 스미스차트의 아주 중요한 장점중 하나가 바로 임피던스와 어드미턴스를 동시에 쉽게 접근할 수 있다는 것입니다.
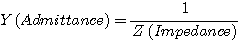
어드미턴스(Admittance)는 아시다시피 임피던스의 역수를 의미하며, 임피던스는 얼마나 신호의 흐름을 방해하느냐의 기준이 되는 것에 반해 어드미턴스는 얼마나 신호를 더 잘 흘러줄 수 있느냐라는 의미가 되지요. 이것은 결국 병렬 회로 구성을 위해 필요한 개념입니다. 직렬에서의 저항은 그냥 줄줄히 더하면 되지만, 병렬일 때는 저항의 역수들을 더해서 그걸 다시 역수를 취해야 한다는 점은 고등학교때도 배우지요? 바로 직렬회로와 함께 병렬회로를 분석하고자 할 때는. 병렬단에서 어드미턴스라는 개념을 쓰는게 더하고 빼기가 훨씬 쉬워진다는 점이 중요합니다.
스미스차트에서 어드미턴스 좌표계는 임피던스 좌표계를 세로축 기준으로 그대로 거울반사시킨 모양새입니다. 그리고 많은 경우 스미스차트는 색상을 달리하여 임피던스차트와 어드미턴스 차트를 동시에 인쇄하여 보는 경우가 많습니다.
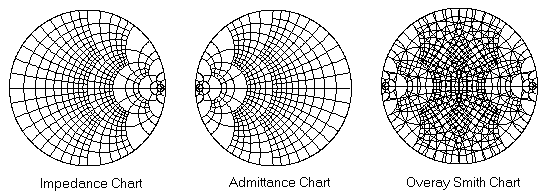
이렇게 겹쳐있는 스미스차트상에서, 해당 임피던스를 어드미턴스로 변환하지 않고(원점대칭) 바로 어드미턴스 좌표계로 읽어서 변환할 수 있기 때문에 아주 편리합니다.다만 두 그래프를 겹쳐놓으면 색상을 다르게 할지라도 좀 어지러워 보인다는 문제점이 있긴 하지만요.. (@.@)
그럼 왜 이런 어드미턴스는 왜또 읽는건지.. 하는 의문이 들 수 있을 겁니다. 이것은 주로 임피던스 매칭에서 필요한 것이므로, 임피던스 매칭에 대한 장에서 자세히 다루도록 하겠습니다. 일단 이런게 있다는 것을 익혀두시길...
![]() Short와
Open
Short와
Open
Short는 신호가 완전히 도통되게 단락되는 경우를 말하고, Open은 말그대로 회로가 끊어져서(열려서) 신호가 통과하지 못하는 상태를 말합니다.
이것은 임피던스의 허수부가 아니라 실수부가 주로 결정하는 문제입니다. 임피던스가 0에 가까울수록 저항성분이 없다는 얘기이므로 신호가 자~알 흐르게되어 short가 됩니다. 반면 임피던스가 수백수천을 넘어 무한 대에 가까워지면 loss가 너무 심해서 신호가 흐르지 못하는 Open 상태가 되어버립니다. 이것은 스미스차트에서 아래처럼 보여집니다.
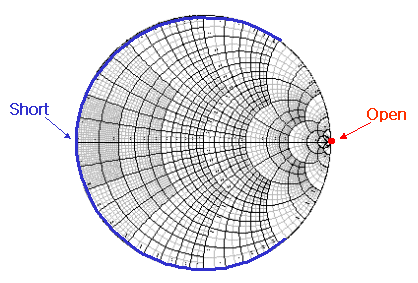
그래서 임피던스 점이 왼쪽에 있으면 낮은 임피던스, 오른쪽으로 가면 높은 임피던스점을 의미하게 됩니다. 이러한 점들은 좌표만 읽을 줄 알아도 바로 알 수 있는 것이므로 외우지 말고 이해하도록 하세요. 처음에 배울 때는 뭐가 뭔지 몰라서 마냥 외우기만하는 경우가 많은데, 임피던스가 0 인 원은 short가 되고, ∞ 인 원은 open이 된다는 것을 잘 음미해보시기 바랍니다.
![]() 이제
시작!
이제
시작!
스미스차트 강의 시리즈 초반에 언급했듯이, 실제적인 활용의 사례나 연습없이는 별로 감이 안오는게 정상입니다. ^^;
이 장에서 설명된 내용은 지금보다는 여러 활용과 실습을 통한 후에 다시 읽어보면 아하~ 하고 더 마음에 와닿을 만한 내용들이 많습니다. 또한 현재까지 스미스차트를 어케어케 쓰고는 있었는데 조금 아리까리했던 분들께는 보다 구체적으로 이해가 될 내용들일 것입니다.
여기서 배운 것은 사용법이 아니라 그냥 읽는법을 배운 것입니다. 진짜 사용법을 배우기 위해 먼저 Smith tool이란 쓸 만한 공개용 소프트웨어에 대해 공부해보도록 하겠습니다.
Copyright by RF designhouse. All rights reserved.