선형성 얘기를 하려는 왜 harmonic얘기부터?? 라고 의아해 하실 지 모르지만, 선형성이란 개념을 짚고 넘어가려면 우선 harmonic을 이해할 필요가 있습니다.
![]() Harmonic
(고조파)의 정의
Harmonic
(고조파)의 정의
하모닉(Harmonic)이란 우리말로는 '고조파'라고 부릅니다. 가끔 고조파와 고주파를 헷갈려 하시는 분들이 있던데 주의하시길!! 고주파는 주파수가 높은 전자기파를 말하며, 고조파는 바로 harmonic을 말하는 것입니다.
Harmonic의 정의는 원천주파수(Fundamental Frequency)의 배수 주파수 성분을 말합니다. 예를 들어 1.2GHz의 Harmonic 주파수는 2.4GHz, 3.6GHz, 4.8GHz... 등이 됩니다.
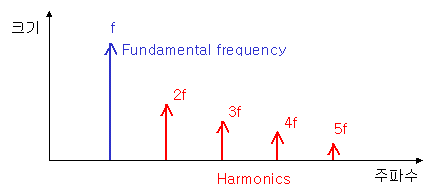
별거 아니죠?
그런데 왜 이런
harmonic이란게 발생하며, 그것이 가진 의미는 무엇일까요?
![]() 생활속의
사례
생활속의
사례
" 모든 것은 주기적이며, 배수적이다
"
예를 들어 여러분이 작년 9월 16일날 결혼했다고 치죠.
그렇다면 1년이 지난 올해 9월 16일에는 결혼 1주기를 기념한 데이트를
할지도 모릅니다. 그리고 그 다음해인 내년에도 뭔가 기념행사를 할
것이지만, 아마도 해가 갈수록 기념하는 경우가 적어지거나 간소화 될
지 모릅니다.
(제가 살아보니 그렇더군요 -_-;;)
세상 모든게 주기적이라는 그런 철학적 논리가 아니더라도, 우리가 접하는 RF는 주기적 변화의 상징 그자체입니다. 주파수(frequency)를 가지고 있는 어떤 주기적 성분은, 그 주파수가 2배, 3배, 4배 쯤 되는 지점에서 뭔가 유사한 특성을 가지게 됩니다. 그리고 그 유사한 특성은 주파수의 배수가 높아질수록 약해집니다. 위의 예처럼, 생활속에서도 그러한 모습을 쉽게 찾을 수 있지요?
![]() 공진을
통한 선형 Harmonic의 이해
공진을
통한 선형 Harmonic의 이해
rectangular cavity의 공진에 대한 예를 한번 보도록 하지요. 네모난 사각 금속상자안에 동축선 프로브등을 통해 AC 신호를 sweep시키면, 그 육면체의 각 변의 길이에 맞게 공진이 발생합니다. 아래의 그래프는 주파수축에서 본 cavity의 S21입니다. 주기적으로 S21이 집중되며, 점점 작아지고 있는 것을 볼 수 있습니다.
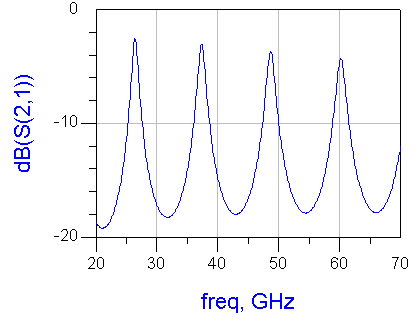
이런 cavity의 공진원리는, 반파장길이와 직접적인 관련이 있습니다. 아래의 그림에서 알 수 있듯이 한주기의 sine 파형의 반, 즉 180도의 위상차를 가진 반파장 길이는 중요한 의미를 갖고 있습니다. 아래의 빨간 동그라미를 취한 점은 신호가 +와 -신호로 바뀌는, 수학적으로 중요한 절점입니다. 실제로 구조적인 공진은 이러한 반파장 단위로 이루어지지요.
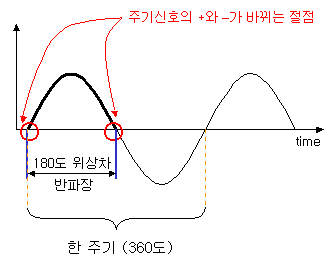
아래는 바로 위의 사각형 공진기에 주기신호가 입사되었을 때 내부에서 발생하는 공진형상을 나타낸 것입니다. 한 구조에서 발생하는 공진성분은, 중요 주파수를 기준으로 여러 배수성분들이 기생적으로 발생하죠. 이렇게 파장수에 따른 공진형태를 분류할 때 우리는 그것을 mode라고 부르기도 하지요. mode 1, mode 2, mode 3 ...
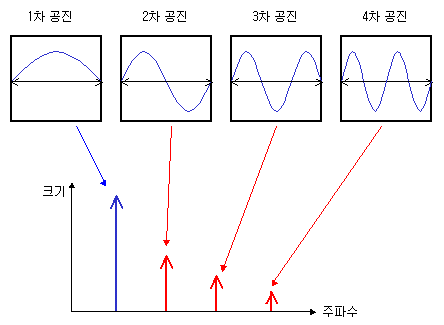
이렇듯 Harmonic은 전기적/물리적 파장과 직접적인 관련이 있습니다. 주파수가 두배로 올라간다는 것은, 파장이 반으로 짧아진 것이기 때문에 파장 두 개분의 길이가 원래 주파수의 파장이 하나일 때와 유사한 특성을 발휘합니다. 다만 harmonic 주파수가 올라갈수록 한 구조물에서 여러파장을 갖고 공진하게 되기 때문에 loss도 늘어나서 반파장에서 공진하는 mode 1보다 에너지가 점점 약해지게 됩니다.
여기서 알 수 있는 중요한 사실은, 뭔가 RF신호를 처리하다보면 그 대상 주파수와 유사한 성질을 가진 배수 주파수 성분들이 나타날 수 있다는 것입니다. 그리고 이것은 전기적/물리적 파수 (wavenumber) 가 배수로 늘어나는 것과 직접적인 관련이 있다는 것이지요! 이 예를 통해, 구조적 크기와, 전기적 파장의 관계에서 자연스럽게 harmonic의 개념을 발견할 수 있습니다.
하지만 이 cavity는 선형적인 동작을 하는 시스템에서 발견가능한 harmonic 주파수들을 보여주는 예입니다. 이것은 fundamental frequency 입력에 의해 발생한 harmonic들이 아니라, 여러 주파수들이 동시에 sweep되었을 때 harmonic하게 공진주파수점이 나타나는 관계를 보여주는 것이지요.
그래서 실제로 우리가 선형화의 관점에서 주로 관심을 가져야 할 harmonic은, 비선형 소자에서의 harmonic입니다. 위의 선형동작을 하는 cavity와 달리 비선형소자에서 발생하는 harmonic은 다른 주파수입력없이 fundamental frequency 하나만 입력해도 발생한다는데 문제가 있습니다.
![]() Nonlinear
Harmonic Generation (비선형 하모닉 생성)
Nonlinear
Harmonic Generation (비선형 하모닉 생성)
잠깐 여기서, 우리가 원래 논하고자 했던 선형성의 의미를 고찰해볼까요? 선형성이 중요한 이유는 시스템이 비선형적이기 때문입니다. 비선형 시스템을 사용할 수밖에 없기 때문에, 어떻게든 그나마 최대한 선형적으로 동작할 수 있게 하느냐의 문제이죠. (선형성이나 비선형성이 궁극적으로 의미하는 바가 무엇인가는 '3장 선형성이 뭐길래' 에서 좀더 꼼꼼히 따져보도록 합니다.)
위의 cavity예제는 선형적 시스템에서 '발견'가능한 harmonic 주파수 성분들입니다. 엄밀한 의미에서 fundamental frequency로부터 발생(generation)된 것들은 아닙니다. 그러나 비선형(nonlinear)소자인 Transistor나 Diode등은, 단 하나의 주파수 입력이 있더라도 harmonic을 생성합니다. 이런면에서 선형 시스템에서의 harmonic과 비선형 시스템에서 말하는 harmonic은 차이가 있습니다. 우리가 주로 관심을 가져야 할 것은, 바로 비선형 소자의 harmonic generation입니다.
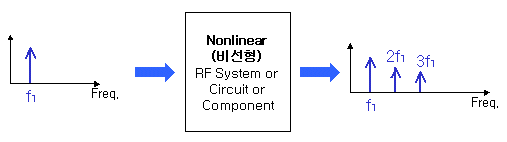
이렇게 원하지 않는 비선형 소자의 harmonic들은 결과적으로 시스템적으로 선형성을 깨뜨리는 주요한 source가 됩니다. 반면 Mixer나 Freuquency Doubler/Multiplier 에 있어서는 주요한 주파수변환의 source가 되기도 합니다.
![]() 비선형 소자는
왜 harmonic을 생성하는가?
비선형 소자는
왜 harmonic을 생성하는가?
자, 그렇다면 왜 비선형소자는 이런 harmonic들이 생성되는지 궁금해야 정상입니다 (^^;) 그렇다면 왜 우리는 Transistor와 Diode를 비선형소자라고 부를까요? 그것은 입출력 전류/전압 특성이 비선형적이기 때문입니다. 그것을 그래프로 나타내자면 아래와 같습니다.
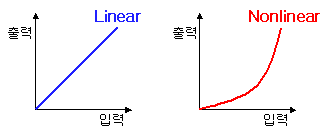
우리가 선형소자, 비선형소자라고 부르는 것은 바로 이런 입출력 특성 때문입니다. 비선형소자는 내부의 반도체소자 물성과 접합의 문제로 인해 이러한 비선형적인 특성을 가집니다. 이러한 비선형 입출력 특성을 수식으로 풀어보면 아래 그림처럼 됩니다. 저 삐뚜루한 비스듬 곡선을 수학적으로 풀면 아래와 같이 제곱식의 조합으로 표현됩니다.
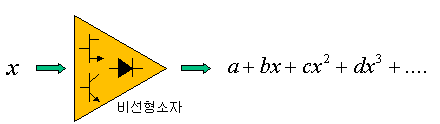
만약 여기서 입력신호 X가, 아래와 같이 주파수를 가진 AC신호라면??
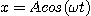 at
at 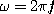
출력은 이런 식으로 구성됩니다. x 대신에 위의 코사인 함수를 넣어볼까요?
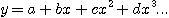
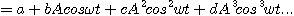
간만에 수식 보니 눈돌아갑니까? 이건 수식으로밖에 증명이 안됩니다. 잠시 고등학교때 지겹게 했던 계산을 다시 해보지요. 위의 cos 대입수식을 각 order별로 풀어보면 아래와 같습니다.
상수항 (Constant ; Zero order)

: DC term을 의미합니다. 주파수가 없으니.
▶ 1승째 항 (First order)

: 이건 그냥 자기 주파수 출력을 말하지요. fundamental frequency입니다.
▶▶ 2승째 항 (Second order)
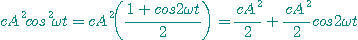
: 어라? 삼각함수 공식에 의거하여 주파수가 없는 DC항과 cos2ωt 라는 성분이 튀어나왔습니다. 이것은 2ω, 즉 2배 주파수에 해당하는 Harmonic 성분입니다.
▶▶▶ 3승째 항 (Third order)

3승의 항을 삼각함수 법칙에 의해 풀어보면 역시.. cosωt 의 fundamental frequency 성분과, cos3ωt 라는 3배주파수의 harmonic성분이 튀어나옵니다.
나머지 4승이후의 항들도 계속 풀어보면, 점점 작아지긴 하지만 줄줄히 fundamental frequency의 배수에 해당하는 harmonic 주파수 항이 나오는 것을 쉽게 알 수 있습니다.
뭐 수식이 복잡하게 증명되긴 했는데, 사실 중요한건 이렇게 비선형 소자를 통과하고 나면 위와 같이 원래 주파수의 배수에 해당되는 harmonic 들이 튀어나온다는 사실입니다. 그것만 알아도 되긴 됩니다 (^^;) RF 시스템에 필수적인 amp, mixer 등은 이런 비선형소자들을 사용해야 하기 때문에 결국 회로와 시스템 전반에 걸쳐 harmonic들이 줄줄이 발생할 수밖에 없는 것이죠.
바로 이러한 비선형성에 기인한 harmonic들이 우리의 주요 관심사입니다. 어쩔 수 없이 발생되기 때문에 운명으로 받아들이고 그것을 어떻게 분석하고 억제하느냐가 관건인 것이죠. 그렇다면 다음으로 Harmonic에서 생성되었으나 Harmonic보다 더 짜증나는 Intermodulation에 대해 알아보도록 합시다.
Copyright by RF designhouse. All rights reserved.