RF 수동회로의 꽃 Filter !
RF 시스템 전반에
걸쳐 가장 많이 사용되는 회로중 하나이며, 매우 다양한 종류와 형태로
구현되는 이 filter란 놈은 언뜻 보면 그리 복잡할 거 없는 단순한 녀석처럼
보입니다. 하지만 막상 뚜껑을 열고보면 꽤나 얘기해야할 테마가 많은,
확실한 주연급배우입니다.
쉬운 듯 방대한 filter의 세계를 전부
다루려면 너무나 할얘기가 많습니다. 여기서는 아주 원초적으로..
쉽게 전체적으로 이해할
수 있도록 순서대로
차근 차근 풀어나가 보도록 하겠습니다. 필터를 한큐에 완전하게 이해하기는
좀 애매하므로.. 여러 각도와 관점에서 들여다 본후 그런 기본 개념들을
조합하여 이해할 수 있도록 서술하였습니다.
![]() Filter를
이해하기 위하여..
Filter를
이해하기 위하여..
이름만봐도 알 수 있듯이 Filter는 입력된 여러 주파수 성분중 원하는 주파수만 통과시키고 나머지는 감쇄시켜 버리는 역할을 합니다. 결국 Filter는 주파수선택을 위해 꼭 필요한 개념이지요.
RF 인이라면 Filter를 피해다닐 수가 없습니다. 수동회로는 물론 능동회로, 시스템에 걸쳐서 단품이건 부속품이건 매칭회로로 존재하건 간에 Filtering 개념이 필요하지 않는 곳은 없으니까요. 일단 RF라 하면 자기가 쓰는 주파수는 정해져있는 법이고, 이렇게 주파수를 선택하려면 반드시!! 필터는 필요합니다.
이런 filter를 이해하기 위한 핵심 키워드는 바로 아래의 세 단어입니다.
Inductance(인덕턴스), Capacitance(캐패시턴스), Resonance(공진)
Filter를 제대로 이해하기 위해서는 반드시
위의 개념들을 익혀야만 합니다. L과 C, 그리고 그 둘에 의한 공진에
filter 메카니즘의 모든 것이 들어있습니다. 그러므로 아래 기초강의
내용을 미리 안보시고 이 글을 읽으신다면, 때수건도 없이 1년만에 목욕하는
것과 같습니다.
▶
RF관점에서
본 L과 C
▶ 공진(Resonance)의
이해
아무리 궁금하고 가려워도 그걸 긁어서 시원하게 해줄 이태리타올이 있어야 되는 법이죠. 물론 1년만에 목욕하면 맨손으로도 때가 잘 밀린다고 주장하신다면 별로 할말은 없습니다 -_-;; 예가 좀 이상하긴 한데.. 여하튼 기초개념없이 회로를 이해한다는 건 순서가 틀린 것입니다. 성급하게 굴지 마시고 꼭 위의 글을 먼저 보시기 바랍니다~
![]() Filter의
S parameter
Filter의
S parameter
필터에 대해 여러각도로 이해하기에 앞서.. 먼저 대표적인 고주파특성그래프인 S parameter 그래프를 읽고 이해할 줄 알아야 할 것입니다. 원초적 기초답게 아주 쌩기초부터.. ^^;
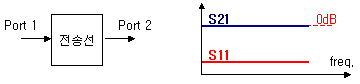
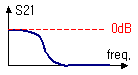
일반적인 선로에 RF 신호를 인가하면, 약간의 선로 손실을 제외하고는 위 그림처럼 깨끗하게 그냥 들어간대로 나올 것입니다. S parameter에서 S21이 0dB란 의미는, 출력/입력의 비가 1이라는 의미입니다. 잘 아시다시피 10* log 1 = 0 이므로, S21이 0dB란 말은 아무 손실없이 입력전력이 출력에 깨끗하게 나온다는 의미입니다. S11이 저 밑에 존재한다는 것은, 반사량이 아주 작다는 것이지요.
이것은 어떠한 주파수선택의 개념없이 그냥 전송만하는 선로일 뿐이니까 당연히 저렇게 나와야 좋은 것입니다. 만약 선로 대신에 필터가 놓이게 되면 그래프가 어떻게 변할까요? (Low pass filter의 예)
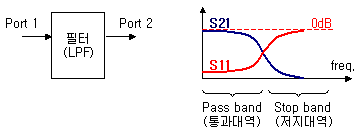
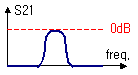
S21이 0dB 근방을 유지하고, S11이 낮은 값을 지칭하는 경우는 해당주파수의 입력 신호가 최소한 반사되며 최대한 출력으로 전달되고 있다는 의미가 됩니다. 즉 통과대역(pass band)에 해당합니다. 반대로 S21은 작고 S11이 0dB 가까이 커지는 경우는 해당주파수의 입력전력이 대부분 반사되어 전달되지 않는다는 의미가 되어 저지대역(stop band)이 되는 것이지요. 이렇듯 특정 주파수는 깨끗하게 통과시켜 주고, 그 이외의 주파수들은 통과시키지 않는 것, 그것이 필터가 하는 역할입니다.
결과적으로 통과대역은 S21은 높고 S11은 작게, 저지대역은 정 반대로 나타나게 됩니다. 너무 쉬운가요? ^^; 그래도 한번정도 정리는 하고 넘어가야 할 것 같아서..
![]() Filter의
종류 1 - 대역특성에 따른 분류
Filter의
종류 1 - 대역특성에 따른 분류
일단 필터가 어떤 종류가 있을런지 구분해보죠.
필터는 정의하기에 따라서 여러 가지 분류법에 의해 구분되는데.. 우선 대역통과 특성에 따른 Filter의 종류를 명확히 짚고 시작해야 할 필요가 있습니다. 잘 알려져있다시피 어느 주파수 대역을 통과키는지에 대한 특성에 따라 필터는 4가지의 종류로 구분할 수 있습니다.
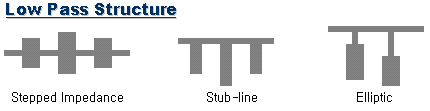
1. LPF (Low Pass Filter : 저역통과 여파기)
|
|
모든
필터의 기본형이라 할 수 있는 것이 바로 이 LPF입니다.
가장 간단한 형태로 구현되어, 이것을 기반으로 여러 가지
형태로 변환하여 다른 종류의 필터를 만들 게 됩니다. |
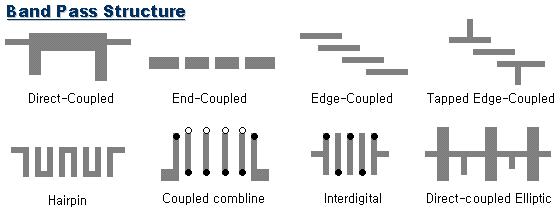
2. BPF (Band Pass Filter : 대역통과 여파기)
|
|
RF
Filter 중에서도 최고의 주연급 배우는 역시 BPF입니다.
여러 주파수를 잘 게 나누어 쓰는 현대 RF에서, 원하는
주파수대역만 정확하게 골라내야 하는 BPF의 역할은 너무나도
중요한 문제입니다. |
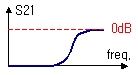
3. HPF (High Pass Filter : 고역통과여파기)
|
|
LPF와
정반대라서 왠지 자주 쓰일 것도 같지만, 실제로는 매우
제한되 용도로 사용되는 필터입니다. 무엇보다 HPF 형태의
필터는 distributed type으로는 구현하기가 어렵다는게
가장 큰 문제입니다. 낮은 주파수의 감쇄를 막아서 LPF로
구현하는 것은 쉽지만, 높은 주파수의 감쇄를 막아서 HPF로
구현하는 것은 어렵습니다. |
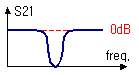
4. BSF (Band Stop Filter, BRF - Band Reject Filter, Notch Filter : 대역저지 여파기)
|
|
말
그대로 BPF와는 정반대로, 모든 주파수대역은 잘 통과시키면서
특정 대역의 주파수만 통과시키지 않는 형태의 필터입니다.
주로 특정 주파수의 유입만 차단하기 위해 사용되며, 보기보다
RF시스템 여러군데에서 곳곳에 유용하게 사용될 수 있습니다. |
자, 필터의 가장 중요한 구분법인 주파수통과특성별 분류를 보았습니다. 이것 말고도 여러 가지 분류가 가능한데, 우선 이와 관련해서 우선 중요한 원리와 특성들을 먼저 살펴보도록 하겠습니다.
![]() 주파수
Filtering의 원리 : L + C = 공진!!
주파수
Filtering의 원리 : L + C = 공진!!
필터란게 만들어질 수 있는 결정적인
원리는 바로 L과 C의 조합에 의한 공진입니다.
L,C의 의미를
다시한번 정의하면..
L (inductance) : 주파수가 올라갈수록
통과가 잘 안되는 특성
C (Capacitance) : 주파수가 올라갈수록 통과가
잘되는 특성
이러한 L,C 의 근본적인 주파수특성만 봐도 알 수 있듯이, 이 두가지의 조합을 잘 꾸미면 원하는 주파수는 잘 통과시키고, 원하지 않는 주파수는 차단해 버릴 수 있습니다. L과 C 하나씩을 이용하여 구현가능한 최소한의 2차 필터 기본형은 아래와 같습니다.
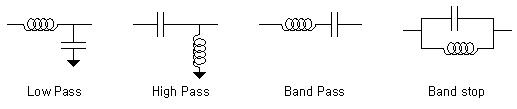
PCB에 직접 땜질하는 lumped element 소자의 L,C는 쉽게 이해가 가지만, 공진필터와 같은 구조적인 형태의 필터는 다른 원리일까요? 아닙니다. 원리는 같습니다.
초심자의 경우에는 L,C 라고 말하면 눈에 보이는 조그만 소자들만 머리속에 떠올리게 됩니다. 그것은 L, C 성분을 특별히 강조해서 만들어진 전용 소자일뿐, 우리가 흔히 inductance/capacitance 라 부르는 개념은 어떤 소자를 지칭하는게 아니라 위와 같은 주파수 통과/감쇄 특성을 가지는 어떤 구조나 현상그 자체를 말하는 것입니다. 구조적인 공진 필터도 결국 L , C 등가회로로 구현이 가능하고, 단지 모양이 달라보일뿐 분석을 해보면 결국 등가의 inductance 성분과 capacitance 성분을 추출해낼 수 있습니다.
여하튼 결국 모든 필터의 근본 원리는 이러한 L, C 성분의 조합이라는 점을 명심하시기바랍니다.
![]() Order
(차수)
Order
(차수)
필터를 논하다보면 차수얘기를 빼놓기
힘듭니다. 영어로는 order 라고 말하죠.
필터를 몇차로 구현하느냐는
특성에 지대한 영향을 미치는 문제입니다. 말로만 하면 잘 이해가 안가니까
아래 그림을 함 보시져. (LPF의 사례)

인덕턴스와 캐패시턴스의 조합으로 표현되는 필터는, 그러한 단위 L,C component( 실제 소자일 수도 있고 L,C가 복합된 물리적인 등가공진구조일 수도 있습니다) 하나하나를 하나의 차(order)로 보는 것입니다.
차수가 높아지면 필터링이 샤프해져서 통과/저지특성이 좋아지지만 삽입손실이나 군지연이 나빠지고 필터의 크기도 커지게 됩니다. 그렇기 때문에 차수를 결정하는 과정의 trade-off가 대단히 중요한 문제가 됩니다. 이것에 대해선 아래에서 좀더 자세히!
![]() 삽입손실과
스커트 (Insertion loss & Skirt)
삽입손실과
스커트 (Insertion loss & Skirt)
필터의 특성을 말하는 가장 중요한 양대 특성은 바로 삽입손실과 스커트입니다. 삽입손실이란, 신호가 필터를 통과하면서 조금씩 손해를 보는 전력을 의미하며, 스커트 특성은 통과대역과 저지대역이 얼마나 구분이 잘되느냐를 말합니다. 삽입손실은 당연히 적을수록 좋은거고, 스커트 특성은 스커트가 더 큰 각으로 바짝 서야지 좋아진다고 말하게 되죠.
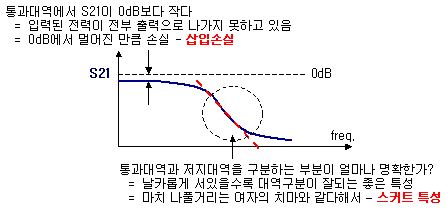
이 두가지는 차수에 의존한 trade off 관계를 갖고 있어서, 어느 한쪽이 좋아지면 나머지 특성은 반대로 나빠지게 됩니다. 왜 그런지 한번 쉽게 이해해볼까요~?
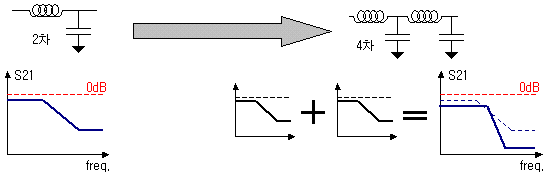
위에서처럼 2차의 필터를 4차의 필터 구조로 바꾸었다고 치지요. 그럼 일단 스커트 특성은 위 그림처럼 더욱 샤프하게 개선될 것입니다. 하나의 필터의 특성이 연달아 중복되면서 저지대역을 더욱 억압하기 때문입니다. 대신에 무언가 나빠지게 될텐데.. 아래 그림을 보시죠.
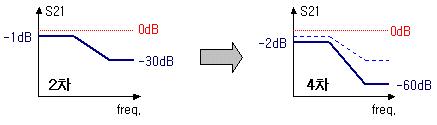
자! 단순하게 한번 생각해볼까요? 신호가 2차 필터를 한번 통과할 때, 통과대역은 -1dB의 loss가 있고, 저지대역에서는 -30dB로 신호가 억압된다고 치지요. 이것이 만약 4차로 확장된다면 똑같은 loss가 통과/저지대역에 한번더 작용할테니, 통과대역에서는 -1 * 2 = -2dB, 저지대역에서는 -30 * 2 = -60dB 가 될 것입니다. 차수가 2차에서 4차로 올라가면서 저지대역의 억압정도가 -30dB에서 -60dB로 되어 통과대역과 저지대역의 차이는 더 커지므로, 대역을 구분하는 스커트 특성은 좋아지겠죠. 하지만 통과대역에서는 신호가 통과하는 길이가 길어지면서 그만큼 loss도 -1dB에서 -2dB가 되듯이 함께 늘어나는건 당연지사 뻔데기입니다.
다만 실제로 차수가 늘어난다고해서 저렇게 단순 더하기 식으로 특성이 딱딱 떨어지지는 않습니다. 그렇게 세상사는게 간단할리야 있겠습니까? ^^; 중요한건... 차수가 늘어난다는 의미는, 유사한 특성변화가 중복되어 위와 같은식으로 억압도가 커지지만 삽입손실이 늘어난다는 점입니다. 이것은 개념적인 이해를 위한 수식계산이며, 실제로는 늘어난 차수만큼의 전체 회로 관점에서 재분석해야 합니다.
어쨌건 이렇게 필터의 길이가 길어지면 시간적인 지연(delay)도 길어지게 되니까 군지연(Group delay) 특성도 나빠지게 됩니다. 무엇보다 필터를 여러 차수로 구현하게 되면.. 돈이 많이 든다는 얘기입니다!! L,C 소자를 이용하는 경우는 소자값 + PCB 면적을 더 차지하게 될거고, 공진구조를 이용한 경우는 공진기가 더 필요하다는 얘기니까 결국은 '돈' 의 관점에서 철저하게 마이너스입니다. 결국 엔지니어로서 이문제를 피해갈 수는 없기 때문에, 원하는 spec을 만족하는 특성을 얻을 수 있는 최소한의 차수를 구현해야 합니다. 제품단가와 특성을 둘다 만족시키도록 하는게 실무 엔지니어의 가장 중요한 지상과제인 것은 어느 분야에서도 마찬가지입니다. ^^;
![]() filter의
종류 2 - 통과특성과 스커트특성에 따른 분류
filter의
종류 2 - 통과특성과 스커트특성에 따른 분류
위의 다양한 필터 특성을 이해하셨다면, 이제 필터 통과특성 자체에 따른 필터 분류를 알아보도록하죠. 이것은 통과대역 형태와 스커트 특성에 따라 분류됩니다. 가장 대표적인 형태 두가지는 바로 butterworth와 Chebyshev 입니다.
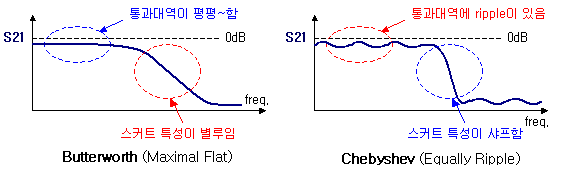
butterworth(버러워쓰) type은 소위 maximal flat (열라평평) 이라 하여, 통과대역의 형태가 가장 평평하게 만들어지는 필터를 말합니다. 하지만 통과대역이 평평하면 스커트 특성을 날카롭게 세우는데 뚜렷한 한계가 있습니다. 가장 단순한 형태의 필터입니다.
Chebyshev(체비세프) type은 다른말로 Equally Ripple (동일잔진동) 이라 하여, 통과대역에 똑같은 크기의 진폭을 갖는 작은 ripple들이 존재합니다. 당연히 이런 ripple들이 있어서 좋을리가 만무하지요! 하지만 작은 ripple이 있는 대신에 스커트 특성이 무척 좋아집니다. 한마디로 옆에서 눌러대서 통과대역이 찌그러진 셈이라고나 할까... 스커트특성이 좋을수록 ripple의 크기는 점점 더 커지는 trade-off 관계가 있습니다. 역쉬 세상엔 공짜가 없다는 걸 다시 한번 증명해주는 현상입니다.
실제로 많은 경우 상업용 필터들은 Chebyshev(체비세프) type 으로 만들어집니다. 상업적 이동통신에서는 잘게 주파수를 나누어 써야 하는데, 통과대역에 다소 ripple 있더라도 대역구분이 명확한 필터를 더 선호하기 때문입니다. 대신, 허용가능한 ripple은 어디까지다라고 정해놓고 씁니다. 필터를 사용할 때 ripple이 0.3dB네 1dB네.. 하는 경우는 바로 이러한 체비세프와 같은형태의 스커트 특성이 좋은필터를 사용한다는 의미이죠.
이러한 통과 특성은, LPF 건 BPF 건 HPF냐와 같은 통과되는 주파수 대역 자체와는 전혀 별개로, 통과대역의 형태와 스커트 특성을 규정하는 별도의 형태를 말하는 것입니다. 즉 butterworth 형태의 LPF 일 수도 있고.. Chebyshev 형태의 BPF 일 수도 있는, 어느 주파수를 통과시키느냐와는 전혀 별도의 분류라는 것이지요. 이러한 통과특성을 결정하는 것은, 필터의 차수에 따른 계수를 어떤 식으로 사용하느냐에 달려 있습니다. 각종 필터책을 참조해보면 여러 종류의 통과특성에 따라 별도로 만들어진 차수별 계수표가 있는데, 여러 차수를 가지는 필터에서 각 차의 소자계수를 해당 특성에 맞게 선택하게 됩니다.
위에 설명된 butterworth type과 Chebyshev type이 가장 많이 사용되지만, 그이외에도 group delay 특성이 우수한 bessel/Gaussian type 과 가장 살벌한 스커트 특성을 가지는 elliptic type 등도 존재합니다. 일단 필터의 통과주파수대역을 정하였다면, 상황에 따라선 이와같이 가장 적절한 통과특성과 스커트형태를 가지는 type을 선택하는 과정도 중요하다 할 수 있습니다.
![]() Group
Delay (군지연)
Group
Delay (군지연)
필터의 주요특성중에 Group delay란 넘이 있습니다.
Group delay (GD) = ∂θ/∂ω
결국 각주파수 ω (=2πf)에 따른 위상의 변화량(dθ)을 말하며, 주파수별로 신호가 지연되는 상대적시간을 의미한다고 보면 됩니다. 이게 먼 말이냐면... 어떤 필터든 간에 신호가 통과하는데 아주아주 작게라도 시간이 걸릴 것입니다. 결국 그런 물리적인 크기가 전기적 파장에 영향을 주어 시간축에서는 신호위상의 지연이 있겠죠.
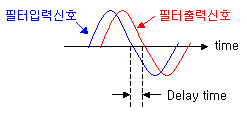
여기서 잠시, 필터가 한 주파수만 다루는게 아니라 특정 주파수대역범위의 신호를 다루는 경우를 생각해보도록 하죠. 그렇다면 넓은 주파수대역의 신호전체에 똑같이 시간지연이 생길테고.. 그렇게 발생한 동일한 시간지연에 의한 위상지연은 주파수마다 다를 수밖에 없습니다. 왜냐? 주파수마다 파장이 다르기 때문에 신호가 지연된 시간은 같아도 그에 의한 위상차는 주파수마다 다르게 적용될 테니까요.
이렇게 되면 나중에 필터를 통과한 주파수대역 신호를 복조할 때.. 에러가 발생할 가능성이 큽니다. 신호 주파수 대역내에서, 서로 다른 주파수별로 각각의 파장에 따라 다르게 지연된 위상으로 인해 전체 신호에 왜곡(distortion)이 생기기 때문이죠. 이러한 현상은 upper band와 lower band로 구별되는 AM(진폭변조)신호의 경우 더 두드러지게 나타납니다.
그래서 filter를 구현할 때 이러한 group delay가 아예 작아지거나, 넓은 주파수대역에서 일정해지도록 만들 필요가 있습니다. 저 위에 설명된 필터통과특성에 따른 type중, time domain 신호특성을 고려한 type 이 바로 Bessel type이나 Gaussian type과 같은 것들입니다. 아래그림 오른쪽의 Group delay 그래프에서 보여지듯이, Bessel type의 필터의 경우 통과대역에서 매우 균일한 Group delay값을 가지며, 주파수 선택특성이 좋은 Chevyshev의 경우는 매우 나쁜 Group delay 값을 가짐을 볼 수 있습니다.
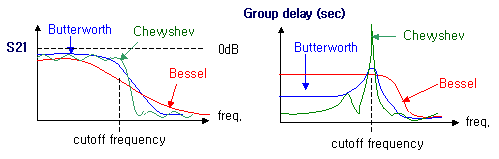
Bessel/Gaussian 과 같은 확률적 계수조합에 의한 필터는, 언뜻보기엔 butterworth랑 비슷하거나 그보다 삽입손실과 스커트 특성이 더 나빠보입니다. 하지만 뭔가 나빠지면 뭔가는 좋아지는 법! 그래서 대신에 넓은 주파수 대역에서 동일한 Group delay 성능을 가지게 됩니다. Group delay 특성이 중요한 필터라면 이런 Bessle type 계수에 따른 차수와 소자임피던스 값을 계산하는게 유리할 것입니다. Group delay 특성은 변복조 방식의 특성에 따라서는 별로 중요하지 않은 특성지표일 수도 있으나, AM 광대역 변조같은 경우라면 매우 중요한 지표가 될 수 있습니다.
![]() Filter의
종류 3 - 구현 형태에 따른 분류
Filter의
종류 3 - 구현 형태에 따른 분류
이번에는 실제로 이러한 L - C 조합에 의한 필터구조를 물리적으로 어떻게 구현하게 되는지에 대해 알아보도록 하겠습니다.
1. Lumped Element
말 그대로.
lead type 혹은 SMD type의 L, C 소자를 PCB에 땜질해서 만들 수 있는
원초적이고 기본적인 필터입니다. 2~3GHz 이하의 주파수에서는 MMIC/RFIC나
PCB상에서 쉽게 구현할 수 있습니다만 3~5GHz 이상으로 주파수가 높아지면
각 소자의 사용제한 주파수인 SRF
에 걸려서 쓸 수 있는 소자가 제한되서 사용이 힘듭니다.
2. Transmission line - Microstrip / Stripline
수
GHz 이상의 경우 lumped element를 사용하기도 힘들어지고.. 정교한
control이 어려울 때, 전송선로를 이용한 필터를 생각해 볼 수 있습니다.
그중 가장 대표적으로 사용되는 것인 Microstrip/Stripline인데, 어차피
두가지는 공식만 다를 뿐 구현하는 방법은 거의 같습니다. Microstrip의
형태일 때는 크게 ① 선로간의 커플링 ② 선로상의
공진 ③ 다중 임피던스 연결 의 원리를 이용하여 필터를 구현하게 됩니다.
이러한 Microstrip 필터의 패턴은 아래와 같이 그 종류가 무척이나 다양한데,
여러 아이디어를 조합하여 흥미로운 필터형태를 만들어내게 됩니다.
(와.. 이것들 그리기 힘들었어요.. ^^;)
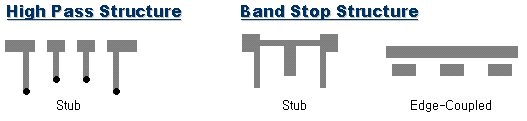
결국 얘네들도 따지고 보면 inductace
와 capacitance의 관계로 등가회로 분석이 가능합니다. 이러한 구조의
필터는 단순한 회로해석으로는 정확한 결과를 얻기가 다소 어렵고, 2.5D
EM tool을 이용하여 설계하고 튜닝하는 경우가 많습니다.
이것에 대해
더 궁금하신 분은 맨 아래에 소개되는 Reah 교수님의 책을 초강추합니다!
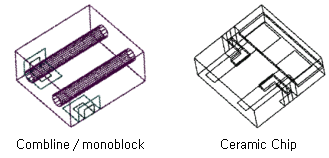
3. Ceramic / dielectric
파장에
따른 공진을 이용하는 구조적 필터로서, 고유전체의 유전체 세라믹을
이용하여 신호의 전기적 파장을 줄임으로써 좀더 compact한 필터를 구현해냅니다.
combline이라 불리우는 단위파장 공진기를 이용하는 경우가 많은데,
별개의 combline을 하나 하나 연결하는 방식과 하나의 유전체 블록으로
구현하는 모노블럭 방식이 있습니다. 그 외에 세라믹 내에 다층 패턴을
이용하여 만드는 세라믹칩필터등이 있습니다. Band pass를 구현하는
일종의 고성능 공진기라고 보면 됩니다. 3D EM tool을 이용하여 설계되는
경우도 많지만, 입출력 포트조건을 조심스럽게 잘 잡아야 한다는 번거로움이
있습니다.
4. Waveguide(도파관)
공진(resonace)현상을 직접적으로 이용하는
경우로서, 크게 금속블럭을 이용한 cavity 방식과 유전체를 삽입하는
ceramic 방식이 있습니다. 도파관 필터는 위성이나 이동통신 기지국의
경우처럼 kW 단위의 대전력을 사용하는 경우에 널리 응용됩니다.
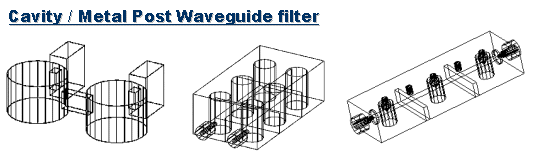
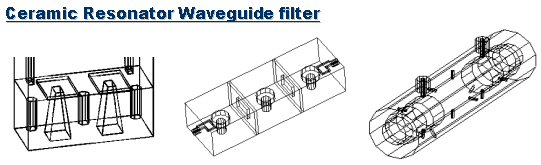
도파관에 구멍을 하나뚫고 나사만 박아도, 도파관의 진행모드 주파수별로 다른 영향을 줌으로써 필터처럼 주파수 선택성이 생깁니다. 이러한 기본적인 도파관의 원리에 입각하여 매우 다양한 아이디어와 방법으로 필터구현이 가능합니다. 상용화된 도파관 필터 자체에 대해선 책에 자세히 나온 경우는 드물고, IEEE의 논문들을 참조하는 것이 좋습니다. 이러한 도파관 필터를 설계할 때는 3D EM tool의 정확도가 비교적 높은 편이라 널리 이용되고 있습니다.
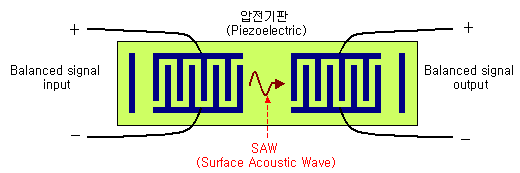
5. Saw (Surface Acoustic Wave)
소형,
경량, 박형을 추구하는 이동통신 단말기와 같은 휴대용 장비의
필터 중 최고봉은 역시 쏘필터입니다. 동일한 성능을 구현하는 경우
LC 필터, 세라믹 필터 등에 비해 가장 작은 크기로 구현이 가능합니다.
원리는 압전물질 표면에 빗살모양의 전극을 어긋나게 배치하면 표면탄성파가
발생되서 그 탄성파주파수와 동조되는 특정 주파수만 통과되고 나머지
주파수는 감쇄된다는 것입니다. 그 작은 구조에 비해 SAW는 매우 샤프한
스커트특성을 갖고 있기 때문에 무선단말기에서 가장 선호되는 필터입니다.
6. 기타
최신 기술인 MEMS,
LTCC,
FBAR
등을 이용한 필터구현에 대한 연구도 계속되고 있습니다.
![]() 마치며
마치며
Filter만큼 매력적인 RF회로소자도 없습니다. 그 방대한 종류와 특성, 형태.. 그리고 수동회로다보니까 능동회로에 비해 튜닝빨이 잘먹혀서 만드는 재미도 쏠쏠합니다. 물론 잘 안나올 때는 괴롭고 속이타긴 마찬가지지만..
필터도 따지고 들자면 꽤 심오하다는 것.. 필터하시는 분들은 다 아실 것입니다. 필터가 뭔지 아직 구체적인 개념이 잘 안잡히신 분들께 이 강의가 조금은 개념확립에 도움이 되셨길 바랍니다. 하지만 분명히 말씀드리자면 여기에 설명된 것들은 그야말로 어버부(Overview -.-;)일 뿐입니다. 지대루 보실려면 꽤나 파고들어야 한다는 점, 명심하시기 바랍니다.
초고주파 필터에 대한 내용은 각종 초고주파 공학책에 기본적으로 다 잘 나와 있습니다. 기타 필터에 대해 좀더 자세히 들여다보고 싶으신분이라면 아래 책을 권하고 싶습니다.
▶Microwave Filters Impedance-Matching Networks, and Coupling Structure (필터 바이블!)G. Matthaei, L. Young, E.M.T. Jones / Artech House
▶HF
Filter Design and Computer Simulation Rhea, Randall W. / Noble
>>
이 책은 기술문서 자료실에 책의 전문이 올라와 있으니 참고하세요
Copyright by RF designhouse. All rights reserved.